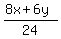> 1
Multiply both sides by 24 to clear the fraction.
8x + 6y > 24
Divide both sides by 2 to simplify
4x + 3y > 12
First we draw the graph of the boundary line which has
equation like the inequality except that we replace the > with =
Boundary line's equation is
4x + 3y = 12
Get the intercepts of (3,0) and (0,4)
Draw the line dotted, not solid, because the inequality symbol is
> and not >, which means that the points on the boundary line
are NOT solutions to the inequality.
All the solutions to the inequality are on one side or the other
of that dotted boundary line.
To determine which side of that dotted line we shade, we pick
a test point on each side of the line, which can be any arbitrary
points as long as they are not on the boundary line.
Suppose we pick the test point (4,5) on the upper side of the
line and (1,1) on the lower side of the line.
We substitute both points in the inequality 4x + 3y > 12
For test pt. (4,5) For test pt. (1,1)
4x + 3y > 12 4x + 3y > 12
4(4) + 3(5) > 12 4(1) + 3(1) > 12
16 + 15 > 12 4 + 3 > 12
31 > 12 7 > 12
TRUE FALSE
So we shade the side of the dotted line for which the
test point is a solution, which is the side that (4,5)
is on, or the upper side, like the green region above
the dotted line:
Shortcuts:
1. You don't really need to get a test point
on but one side of the line, because if it tests TRUE,
it is a solution, so you shade that side. If it tests
FALSE, it is NOT a solution so the solutions are all on
the other side of the line. (The reason I used two
test points was to show you what would happen if you
picked one on either side).
2. If the line does not go through the origin then you
can pick the origin (0,0) as a test point, since 0 is
so easy to work with you can probably substitute it in
your head.
Edwin
(