Question 73840This question is from textbook Algebra and Trigonomerty
: Trigonometry-basics/73819 (2007-03-08 13:33:50):
I am studying DeMoivre's Theorum in Aplications of Trigonometry, I was asked to find the real and complex solution to the equation 
Possible answers
a. -2,2,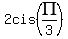
b. 2,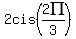 , ,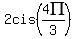
c. -2,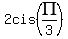 , ,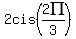
d. 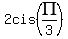 , ,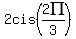 , ,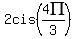 This question is from textbook Algebra and Trigonomerty
This question is from textbook Algebra and Trigonomerty
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am studying DeMoivre's Theorum in Aplications of Trigonometry, I was asked to find the real and complex solution to the equation 
Possible answers
a. -2,2,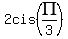
b. 2,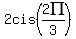 , ,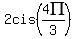
c. -2,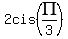 , ,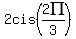
d. 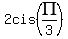 , ,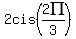 , , 2cis(4PI/3)}} 2cis(4PI/3)}}
-----------
The polar form for (0,8) is z = 8cis(0+2(pi)n) where n=0,1,2,3,...
The cube root is (cube rt 8)cis((2/3)(pi)n) where n=0,1,2,...
For n=0 the cube root is 2cis(0) = 2*1 = 2
For n=1 the cube root is 2cis((2/3)(pi))
For n=2 the cube root is 2cis((4/3)(pi))
-----------
These are in answer "b".
Cheers,
Stan H.
|
|
|