|
Question 737426: if a right circular cone intersects a plane that goes through both nappes of the cone, but not through the vertex, the resulting curve will be an
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the angle of the plane is 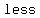 than the angle of the cone, then the intersection is a than the angle of the cone, then the intersection is a 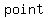 . .
If the angle of the plane is 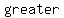 than the angle of the cone, then the intersection is than the angle of the cone, then the intersection is  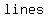 intersecting at the vertex. intersecting at the vertex.
If the plane insersects at 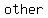 than the than the  , then the intersection is a , then the intersection is a 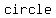 when the plane is when the plane is 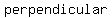 to the cone's axis, an to the cone's axis, an 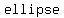 when the plane's angle is when the plane's angle is 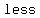 than the cone's angle, a than the cone's angle, a 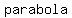 when the planes's angle when the planes's angle 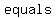 the cone's angle, and two the cone's angle, and two 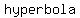 's in the last case. 's in the last case.
If a right circular cone is intersected by a plane so that the intersection goes  the cone's the cone's  as well as an as well as an 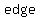 of each nappe, the shape produced is a of each nappe, the shape produced is a 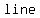 . .
in your case, if a right circular cone intersects a plane that goes through both nappes of the cone, but not through the vertex, the resulting curve will be a 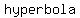
|
|
|
| |