Question 737271: Dear : The tutor
I cant interpret this question ,kindly help me out
How many different triangles can be made with a perimeter of 12matches.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The perimeter of a triangle can be found using:
 , where , where  , ,  , and , and  are the lengths of the sides of the triangle. are the lengths of the sides of the triangle.
You also have the rules:


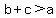
These are true for all triangles.
The most important thing to be kept in mind is the triangle inequality theorem that says that the sum of any two sides is 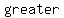 than the third side than the third side
If the sides do  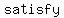 this theorem, then the triangle is this theorem, then the triangle is  
this is also good to remember:
first triangle among many triangles with perimeter  , the most famous is the , the most famous is the 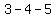 triangle, the triangle with sides triangle, the triangle with sides  , ,  , and , and  (or a similar one.) Since (or a similar one.) Since  , we are assured by the converse of the Pythagorean theorem that the , we are assured by the converse of the Pythagorean theorem that the 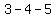 triangle is right. triangle is right.
so, first solution is 
Keeping this in mind we get the following combinations:
 ..... .....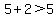 .. ..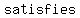 theorem, the triangle is theorem, the triangle is 
 .... ....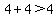 .. .. theorem, the triangle is theorem, the triangle is 
so, if  , the possible triangles, written , the possible triangles, written 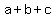 , are: , are:



|
|
|