Question 73680This question is from textbook college algebra
: I need to know if I have done these right!! Thank you so much!!
) Given a line containing the points (1,3), (2,4), (3,5) determine the slope-intercept form of the equation, give one additional point on this line and graph the function.
Show your work here: y2-y1/x2-x1= -4,-6
Give one additional point in (x,y) form that would fall on this line: 4,6
This question is from textbook college algebra
Found 2 solutions by jim_thompson5910, bucky:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 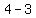 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 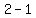 to get to get 
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Distribute Distribute 
 Multiply Multiply  and and  to get to get  . Now reduce . Now reduce  to get to get 
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
So we know the equation is  . Let's plug in another x value. If we let x=4 then: . Let's plug in another x value. If we let x=4 then:



So another point on this line is (4,6)
So yes you did this right. You just need to find the equation and graph it.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm sorry it took so long for me to get to your problem.
.
The slope-intercept form of an equation is:
.
y = mx + b
.
where m, the multiplier of x, is the slope of the graph, and b is the point on the y-axis where
the graph crosses.
.
So let's find the slope. You have the equation correct for finding the slope. That equation is:
.

.
We know that all three of the given points are on the line. All we have to do is identify
one of the points as 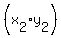 and another of the points as and another of the points as 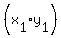 . .
.
It's a little easier to see if we choose as 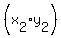 a point that is to a point that is to
.
the right of the point we call 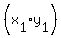 . It doesn't have to be that way because it . It doesn't have to be that way because it
will work out the same no matter what.
.
Anyhow let's choose as 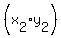 the point (3,5). By comparison, that means the point (3,5). By comparison, that means
 and and  . .
.
Now let's choose as 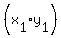 the point (1,3). By comparison of these two the point (1,3). By comparison of these two
that means  and and  . .
.
Then all we do to calculate the slope is to substitute these 4 values into the slope equation
as follows:
.

.
So we have the slope of m = 1. Plug that value of m into the slope intercept form of the
equation and you get:
.
 . .
.
To solve for b, all we need to do is to take one of the given points and plug its x and y
values into the equation  . Then we can solve for b. For example, . Then we can solve for b. For example,
let's take the point (1,3) that we were given. Plug 1 in for x and 3 in for y and the
slope intercept equation becomes  . Solve this by subtracting 1 from both . Solve this by subtracting 1 from both
sides to get:
.

.
Then take this value for b and plug it into the slope intercept form of  and and
you have the final version of the slope intercept form as being:
.

.
Next you said that you thought the point (4,6) was on the graph. Let's check that out by
putting 4 into our slope intercept equation for x and 6 in for y and see if the equation
is still true. When we do the substitution we get:
.

.
Well, that certainly is true, so your point of (4,6) IS on the graph.
.
Hope this helps you to understand the first part of the problem a little better.
|
|
|