SOLUTION: I am trying to find all real and imaginary zeros for the equations: (9x^3+9x^2-19x-7) & (7x^3+5x^2+26x-8) I am more interested in finding how to solve then the solutions themsel

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I am trying to find all real and imaginary zeros for the equations: (9x^3+9x^2-19x-7) & (7x^3+5x^2+26x-8) I am more interested in finding how to solve then the solutions themsel      Log On


   

Question 73678: I am trying to find all real and imaginary zeros for the equations: (9x^3+9x^2-19x-7) & (7x^3+5x^2+26x-8) I am more interested in finding how to solve then the solutions themselves. I can find no factors to divide into the equations! I am usually very good at these but was given these in class and can't find out how to solve them?! VERY Frustrating! Thanx
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Well you sure did pick a hard problem to tackle, I'll see what I can do to help.
9x%5E3%2B9x%5E2-19x-7=0Start with the given polynomial
9x%5E3%2B9x%5E2-18x-x-6-1=0Rewrite the polynomial in terms that are in common with the rest of the polynomial. For instance, 18 is divisible by 6. These tricks are somewhat difficult since there are no set rules for when or how you use them.
%289x%5E3%2B9x%5E2%29%2B%28-18x-6%29%2B%28-x-1%29=0Start grouping common terms
9x%5E2%28x%2B1%29-6%283x%2B1%29-%28x%2B1%29=0Factor out GCF of each grouped term. Notice how we have a common factor of x+1. We can subtract like terms (it's like saying y=x+1 and 9x^2y-y=(9x^2-1)y)
9x%5E2%28x%2B1%29-%28x%2B1%29-6%283x%2B1%29=0
%289x%5E2-1%29%28x%2B1%29-6%283x%2B1%29=0
Now factor the (9x^2-1) term to get (3x+1)(3x-1) notice the common term of 3x+1. Add these like terms.
%283x%2B1%29%283x-1%29%28x%2B1%29-6%283x%2B1%29=0
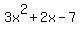%28%283x-1%29%28x%2B1%29-6%29%283x%2B1%29=0So if you use synthetic division, you will find that 3x+1 is a factor and x=-1/3 is a zero. You can use this information to find the other zeros. When you use synthetic division, you will get 3x%5E2%2B2x-7 which is a factor (ie %283x%5E2%2B2x-7%29%283x%2B1%29=9x%5E3%2B9x%5E2-19x-7
Now use the quadratic formula on 3x^2+2x-7 to find the other zeros
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 3x%5E2%2B2x%2B-7+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%282%29%5E2-4%2A3%2A-7=88.

Discriminant d=88 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-2%2B-sqrt%28+88+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%282%29%2Bsqrt%28+88+%29%29%2F2%5C3+=+1.23013858660781
x%5B2%5D+=+%28-%282%29-sqrt%28+88+%29%29%2F2%5C3+=+-1.89680525327448

Quadratic expression 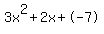3x%5E2%2B2x%2B-7 can be factored:
3x%5E2%2B2x%2B-7+=+3%28x-1.23013858660781%29%2A%28x--1.89680525327448%29
Again, the answer is: 1.23013858660781, -1.89680525327448. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+3%2Ax%5E2%2B2%2Ax%2B-7+%29

So your zeros are x=-1/3, x=1.23014, and x=-1.89681
Feel free to ask about any step. Hope this helps.