SOLUTION: (y^2/3) ^3/4 Simplify

We are given this expression  (y^(2/3))^(3/4)  to simplify.


We can consider it as a formula to calculate a value, like a machinery, or as an algorithm, or as a function.


Then the domain of this function is the set of all real numbers, 
     including positive numbers, negative numbers and 0 (zero).



According to Algebra rules, we should multiply the indexes.


So, if 'y' is non-negative,  y >= 0,  then it is simplified to


    y^((2/3)*(3/4)) = y^(1/2) = .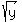


But if 'y' is negative,  then this formula is like a lame horse, because

the left side expression is defined at negative real values of 'y', while the right 

side, 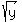 ,  is not defined at negative values of 'y'.


So, if we want formula  y^((2/3)*(3/4) = 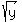  be valid for negative  'y',  too,
we should modify it this way 

    y^((2/3)*(3/4)) = .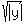


Then both sides will be identical over the whole domain of all real numbers.