Question 736363: Is 12,40,68,96 sequence geometric or arthmetic? If possible what is the common ratio or difference
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! For 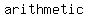 sequences, the common difference is sequences, the common difference is  , and the first term , and the first term  is often referred to simply as " is often referred to simply as " ". Since you get the next term by adding the common difference, the value of ". Since you get the next term by adding the common difference, the value of  is just is just 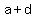 . The third term is . The third term is  . The fourth term is . The fourth term is  . Following this pattern, the . Following this pattern, the 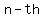 term an will have the form term an will have the form
 . .
For 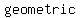 sequences, the common ratio is sequences, the common ratio is  , and the first term , and the first term  is often referred to simply as " is often referred to simply as " ". Since you get the next term by multiplying by the common ratio, the value of ". Since you get the next term by multiplying by the common ratio, the value of  is just is just 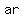 . The third term is . The third term is  . The fourth term is . The fourth term is  . Following this pattern, the . Following this pattern, the 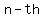 term an will have the form term an will have the form
 . .
in your case  , , , ,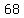 , ,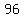 sequence is have the form sequence is have the form
common difference is 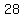 and the greatest common divisor is and the greatest common divisor is 
first term is  and if divided by and if divided by  , we get , we get  that could be written as that could be written as 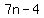 starting with starting with  and up and up
so, the recursive formula is:

and this is 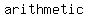 sequence sequence
|
|
|