Question 736251: a. find the value of the objective function at each corner of the graphed region.
b. use the values to determine the maximum value of the objective function and the values of x and y for which the the max occurs
Objective function
z=7x+11y
Constraints
x is greater than or equal to 0 and y is greater than or equal to 0
x+y is less than or equal to 11
x+3y is less than or equal to 18
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  means that we will be working in a region to the right of the line means that we will be working in a region to the right of the line  (the y-axis) and maybe including part of the y-axis (if not ruled out by any other constraint) (the y-axis) and maybe including part of the y-axis (if not ruled out by any other constraint)
 and means that we will be working in a region above the line and means that we will be working in a region above the line  (the x-axis) and maybe including part of the x-axis (if not ruled out by any other constraint) (the x-axis) and maybe including part of the x-axis (if not ruled out by any other constraint)
So far we are limited to the first quadrant.
 means that we will be working on the line or on one side of the boundary line means that we will be working on the line or on one side of the boundary line
 and since and since 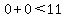 , ,
the point with  and and  (the origin) has not been rules out yet. (the origin) has not been rules out yet.
The boundary line  is easy to graph because is easy to graph because
when   so the point (0,11) is on the line, and so the point (0,11) is on the line, and
when   so the point (11,0) is on the line too. so the point (11,0) is on the line too.
With those 2 points we can draw the line (or at least the part we care about) and we realize that we are constrained to work within the triangle below.

 means that we will be working on the line or on one side of the boundary line means that we will be working on the line or on one side of the boundary line
 and since and since 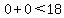 , ,
the point with  and and  (the origin) is not ruled out. (the origin) is not ruled out.
The boundary line  is easy to graph because is easy to graph because
when   --> -->  so the point (0,6) is on the line, and so the point (0,6) is on the line, and
when   so the point (18,0) is on the line too. so the point (18,0) is on the line too.
We can draw the line based on those 2 points.

A region limited by linear inequality constraints is usually a polygon. The maximum of a linear function in such a region must happen at one of the vertices or all along a side (a segment connecting two vertices). We just have to see what happens at the vertices.
The region we will be working on is part of the first quadrant (including parts of the x-axis and the y-axis an only the part that is on the same side of both lines as the origin. So it is the quadrilateral OABC.
We know the coordinates of O(0,0), A(0,11), and C(6,0),
We just have to find the coordinates of B.
Since B is on line  and on line and on line  we need to solve the system we need to solve the system

If we had graphed it on grid paper, we would realize that the lines seem to intersect at {3.5,7.5) or ( , ,  ) and could verify that those coordinates indeed satisfy both equations, We would say that we solved the system by graphing. ) and could verify that those coordinates indeed satisfy both equations, We would say that we solved the system by graphing.
Otherwise, it is easy to solve the system by substitution or elimination.
Now it is a question of calculating the value of  for points O, A, B, and C: for points O, A, B, and C:
At O,  so so 
At A  and and  so so 
At B  and and  so so 
At A  and and  so so 
So the maximum of  happens at point A, happens at point A,
where  , and the coordinates of point B are what we found before we started drawing lines: , and the coordinates of point B are what we found before we started drawing lines:
 and and 
|
|
|