Question 735913: Please help me finish this problem
Solve the system of equations using matrices. Thank you
3x-y-2z=1
4x+2y+z=5 >
6x-2y-4z=9
3 -1 -2=1
4 2 1 = 5
6 -2 -4=9
R1=(1/3)R1
1 (-1/3) -6=1/3
4 2 1=5
6 -2 -4=9
R2=-4R1+r2
1 (-1/3) -6=(1/3)
0 (10/3) 25=(11/3)
6 -2 -4=9
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! given:
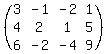
Row operation
1:
 ....multiply the 1st row by 1/3
=> 
Row operation
2:
.........add -4 times the 1st row to the 2nd row...=> 
Row operation
3:
..............add -6 times the 1st row to the 3rd row=>.. .
Row operation
4:
 ....multiply the 2nd row by 3/10..=>...
Row operation
5:
...........multiply the 3rd row by 1/7...=>...
Row operation
6:
 .....add -11/10 times the 3rd row to the 2nd row...>...
Row operation
7:
 ....add -1/3 times the 3rd row to the 1st row...=>...
Row operation
8:
matrix( 1, -1 / 3, -2 / 3, 0,
0 , 1 , 11 / 10, 0,
0, 0, 0, 1
)
)}}}.......add 1/3 times the 2nd row to the 1st row....=>
matrix( 1, 0 , -3/ 10, 0
0 , 1, 11/ 10 , 0,
0 , 0, 0, 1
)
)}}}
so, your solutions ae:  ,  , and 
|
|
|
