Question 735802: Here is the problem: A soccer team has 16 players. How many ways can the coach choose a starting team of 11 players?
I have been working on this problem for forever and still am having trouble solving it. Here's what I came up with but I know I'm doing something wrong.
16!/11!(16-11)! then i write it all out:
________________ <--this is the fraction divider sign thing haha
11! (16-11)!
16x15x14x13x12x11x10x9x8x7x6x5x4x3x2x1
_______________________________________
11x10x9x8x7x6x5x4x3x2x1x(5x4x3x2x1)
it gives me some bizarre number. If you could show how to do the work correctly to get an answer that actually makes sense and explain where I went wrong that would be great. Thanks.
Found 2 solutions by rothauserc, Edwin McCravy:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! This is a combination problem, that is, how many combinations of 16 players taken 11 at a time are there? So we have
the following formula to evaluate
16! / 11! * (16 - 11)! we use the combination formula because order does not matter in this problem
reducing the above formula we get
(16*15*14*13*12) / 5*4*3*2*1
further reduction gives us
8*15*14*13 / 5 = 4368 combinations
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
You need a simpler formula that won't bog you down.
Although 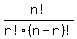 is a correct formula, and is the one given in most
books, it often causes a lot of grief because you often have to write a very
long list of factors as you did above, and many of them will cancel out.
A better though equivalent formula that will give the same answer
is this:
The number of ways to choose R combinations out of N is:
N(N-1)(N-2)...( ) <-- until there are R factors)
—————————————————
R(R-1)(R-2)...2*1 <-- there will be R factors here for R!
So there will be the same number, R, of factors on the top as on the bottom.
Now we'll even make it easier anytime we are choosing more than half of
the number to choose from, as we are in this problem:
Since 11 is more than half of 16, it's easier to look at the problem this
way. Every time we choose 11 players, we choose 5 to NOT PLAY on the team.
So choosing 11 to play is the same as choosing the 5 not to play, so it's
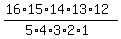Notice I just started with 16 and came down *15*14, etc. until I had 5 factors
on the top and of course there will by 5 factors on the bottom with 5!. Now
you can cancel the 5 into the 15, the 4*3 into the 12 and the 2 into the 14.
And you'll end up with 16*3*7*13 or 4368, same as the other tutor got.
Edwin
|
|
|
