SOLUTION: Mr. T owns a barn that is 10 feet by 20 feet. He has a dog that is a pain and keeps escaping from his yard. So he puts a stake I to the ground 5 feet from the edge of the barn as s

To find the playing area for the dog, we will need the equation for the 
area of a triangle, A = .5bh, b = the base, and h = the height, and the 
area of a sector of a circle,  A = 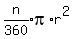, where n is the number of 
degrees in the central angle of the sector, and r is the radius.

The playing area consists of 4 parts:

1. Triangle IAD, which has area .5(5)(10) = 25 square feet.
2. The sector with center I, enclosed by the red arc from E
clockwise to F.  It has center I. and radius 30'. We calculate
the angle AID from tan(AID)=, so angle AID = 63.435°,
and the large sector has central angle 360°-63.435° or 296.565°.
The area of the large sector is 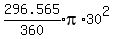 = 2329.216
3. The sector with center D, enclosed by the green arc from F
clockwise to C.  It has center D. We calculate its radius DF by 
subtracting the hypotenuse ID from IF.  The hypotenuse ID is found 
by the Pythagorean theorem: 
ID² = IA² + AD²
ID² = 5²+10²
ID² = 25+100
ID² = √125
 ID = √25·5
 ID = 5√5
 ID = 11.180
So radius DF is 30-11.180 = 18.820. Its central angle is the same as
angle AID because transversal FI cuts parallel lines DC and IE.
So the sector bounded by the green arc has area 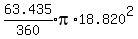 = 196.065 square feet.

4. The sector with center B, enclosed by the blue arc from E
counter-clockwise to G.  It is a quarter of a circle with radius
5, and a central angle of 90° so its area is ,
or 19.635 square feet.

Adding them up, we get

  25      square feet from the triangle
2329.216  square feet from the largest sector
 196.065  square feet from the sector at the top
  19.635  square feet from the sector on the right
---------
2569.916  square feet.

Round that to 2570 square feet. 

Edwin