SOLUTION: solve log3(x-3) + log3(x+2) = log3 6

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: solve log3(x-3) + log3(x+2) = log3 6      Log On


   

Question 734837: solve log3(x-3) + log3(x+2) = log3 6
Found 2 solutions by rothauserc, MathTherapy:
Answer by rothauserc(4718) About Me  (Show Source):
You can put this solution on YOUR website!
note that all log bases are the same (namely 3), so we have
x-3 + x+2 = 6
2x - 1 = 6 and
2x = 7 and x = 3.5

Answer by MathTherapy(10704) About Me  (Show Source):
You can put this solution on YOUR website!
solve log3(x-3) + log3(x+2) = log3 6
************************************
The other person's statement that if "all log bases are the same (namely 3)", then: x-3 + x+2 = 6
                                                                                    2x - 1 = 6 and
                                                                                    2x = 7 and x = 3.5, is a FALLACY!
He couldn't be more WRONG!! If he'd checked, he would've seen that 3.5 doesn't: make sense
                                                                                make the equation TRUE!

The smaller log argument, x - 3 "tells" one that x - 3 MUST be > 0. So, x - 3 > 0____x > 3
We then get: log+%283%2C+%28x+-+3%29%29+%2B+log+%283%2C+%28x+%2B+2%29%29+=+log+%283%2C+%286%29%29, with X > 3
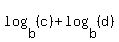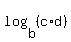                  log+%283%2C+%28x+-+3%29%28x+%2B+2%29%29+=+log+%283%2C+%286%29%29 ----- Applying log+%28b%2C+%28c%29%29+%2B+log+%28b%2C+%28d%29%29 = log+%28b%2C+%28c%2Ad%29%29
                    (x - 3)(x + 2) = 6 ------ Applying c = d, if log+%28b%2C+%28c%29%29+=+log+%28b%2C+%28d%29%29
                          x%5E2+-+x+-+6+=+6
                       x%5E2+-+x+-+6+-+6+=+0
                         x%5E2+-+x+-+12+=+0
                    (x - 4)(x + 3) = 0
                     x - 4 = 0      OR     x + 3 = 0    
                         x = 4      OR     x = - 3

As stated above, x MUST be > 3, so ONLY x = 4 is ACCEPTABLE. This makes x = - 3, an EXTRANEOUS solution to this
equation, and is therefore IGNORED/REJECTED.