Question 734185: Find a formula for a fourth degree polynomial with roots 1,3,5,-1,-3,-5 and p(0)=30
Found 4 solutions by josgarithmetic, KMST, Lightning_Fast, ikleyn:
Answer by josgarithmetic(39621)   (Show Source): (Show Source):
You can put this solution on YOUR website! A polynomial function of degree four will have no more than four roots. You listed six required roots for the function which you want to find. This is impossible.
Did you really mean, ".. .for a sixth degree polynomial..."?
or did you list more roots than you intended?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sixth degree polynomial with roots 1,3,5,-1,-3,-5 and p(0)=30 is
 or or 
For  to be a root, the factorization should include the factor to be a root, the factorization should include the factor 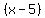
For  to be a root, the factorization should include the factor to be a root, the factorization should include the factor 
Both of those factors multiplied together make

Similarly, if  and and  are roots, the factorization must include are roots, the factorization must include 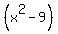 , and for roots , and for roots  and and  we need to include we need to include 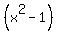 as a factor. as a factor.
With those factors, we get a sixth degree polynomial and there is no room for any other factor with x, but we have to figure out what is the constant factor  that will be the leading coefficient in the polynomial we are looking for that will be the leading coefficient in the polynomial we are looking for

for 
 so so
 ---> --->  --> --> 
Answer by Lightning_Fast(78)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can also do the following:
{{ f(x) {x^2-1)*(x^2-9)*(x^2-25)}}}

F of 0 must be equal to 30
x is the factor that mades the function go though (0,30), similar to the a in the above example
Do algebra and get

Plug the value back into the modified equation and get:
{{ f(x) {x^2-1)*(x^2-9)*(x^2-25) +255}}}
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There is NO such a polynomial p(x) of the degree 4 with 6 listed roots and p(0) = 30.
Such a polynomial does not exists.
The answer by "Lightning_Fast" is WRONG and DOES NOT MAKE SENSE.
|
|
|