Question 733800: Find a polynomial f(x) of degree 4 that has the indicated zeros and satisfies the given condition: -1, 2, 3i; and f(-2)=10
I'm kind of stuck with the 3i in the question. Can someone shed some light on how would I get rid of the i in 3i?
Found 2 solutions by 11anthony, Edwin McCravy:
Answer by 11anthony(1)   (Show Source): (Show Source):
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
-1, 2, 3i; and f(-2)=10
Since 3i is a solution, its conjugate -3i is also a solution.
[Note that since 3i is really 0+3i, its conjugate is 0-3i, which
is -3i]
So we start with
x = -1; x = 2, x = 3i, x = -3i
Get 0 on the right side of each:
x+1 = 0; x-2 = 0 x-3i = 0, x+3i = 0
Myltiply all the left and right sides together. The right side
will just be 0:
(x+1)(x-2)(x-3i)(x+3i) = 0
Multiply both sides by a constant k, and the left
side will be f(x) if we have the right value for k
f(x) = k(x+1)(x-2)(x-3i)(x+3i)
Multiply the first two and the last two factors
f(x) = k(x²-2x+1x-2)(x²+3ix-3ix-9i²)
f(x) = k(x²-x-2)(x²-9i²)
Now since i² = -1, -9i² = -9(-1) = +9
f(x) = k(x²-x-2)(x²+9)
Multiply those two parentheses together:
f(x) = k(x4+9x²-x³-2x²-9x-18)
Collect like terms:
f(x) = k(x4-x³+7x²-9x-18)
Now we can find k because we are given f(-2)=10
We substitute x=-2
f(-2) = k((-2)4-(-2)³+7(-2)²-9(-2)-18)
f(-2) = k(16-(-8)+7(4)+18-18)
f(-2) = k(16+8+28)
f(-2) = k(52)
We substitute 10 for f(-2)
10 = k(52)
 = k = k
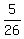 = k
Substitute for k in:
f(x) = k(x4-x³+7x²-9x-18)
f(x) = = k
Substitute for k in:
f(x) = k(x4-x³+7x²-9x-18)
f(x) = 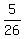 (x4-x³+7x²-9x-18)
f(x) = (x4-x³+7x²-9x-18)
f(x) = 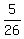 x4 - x4 - 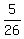 x³ + x³ +  x² - x² - 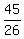 x - x - 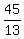 Edwin
Edwin
|
|
|