SOLUTION: what is the area of a regular pentagon with a side length of 7 feet and a length from the center to a vertex of 6 feet

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: what is the area of a regular pentagon with a side length of 7 feet and a length from the center to a vertex of 6 feet      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 733440: what is the area of a regular pentagon with a side length of 7 feet and a length from the center to a vertex of 6 feet
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Connecting the center to the vertices, you would split that pentagon into 5 congruent isosceles triangles with bases measuring 7 feet and legs measuring 6 feet.

We just have to calculate the are of one such triangle and multiply times 5.

If you are not supposed to know about trigonometric ratios/functions, there are 2 options to calculate that area:
You could use Heron's formula if you have learned about it.
Since the altitude splits that isosceles triangle into two congruent right triangles, you could use the Pythagorean theorem to calculate the height 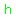green%28h%29.

USING THE PYTHAGOREAN THEOREM:
In a right triangle the lengths of the legs, squared, add up to the square of the hypotenuse.
3.5%5E2%2Bh%5E2=6%5E2 or %287%2F2%29%5E2%2Bh%5E2=6%5E2<-->49%2F4%2Bh%5E2=36
From there we get h:
49%2F4%2Bh%5E2=36 --> h%5E2=36-49%2F4 --> h%5E2=144%2F4-49%2F4 --> h%5E2=95%2F4 --> h=sqrt%2895%2F4%29 --> h=sqrt%2895%29%2F2
Then we calculate the area of a triangle as
area=base%2Aheight%2F2 or area=%281%2F2%29%2Abase%2Aheight
In this case area=%281%2F2%29%2A7%2Asqrt%2895%29%2F2 --> area=7sqrt%2895%29%2F4
The area of all 5 triangles forming the pentagon is
5%2A%287sqrt%2895%29%2F4%29=highlight%2835sqrt%2895%29%2F4%29=highlight%28about85.3%29 (rounding)

USING HERON'S FORMULA:
Heron's formula uses the lengths (a, b, and c) of the sides of a triangle, and its semiperimeter,
s=%28a%2Bb%2Bc%29%2F2
to calculate the area of the triangle as
area=sqrt%28s%2A%28s-a%29%2A%28s-b%29%2A%28s-c%29%29
In this case,
s=%286%2B6%2B7%29%2F2=19%2F2
area=sqrt%2819%2F2%2A%2819%2F2-6%29%2A%2819%2F2-6%29%2A%2819%2F2-7%29%29
area=sqrt%2819%2F2%2A%2819%2F2-12%2F2%29%2A%2819%2F2-12%2F2%29%2A%2819%2F2-14%2F2%29%29
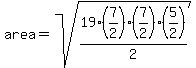
area=sqrt%2819%2F2%2A%287%2F2%29%2A%287%2F2%29%2A%285%2F2%29%29
area=sqrt%28%2849%2F16%29%2819%2A5%29%29 --> area=sqrt%2849%2F16%29%2Asqrt%2819%2A5%29%29 --> area=%287%2F4%29%2Asqrt%2895%29%29
Multiplying the area fiound for one triangle times 5, we find the area of the pentagon as
5%2A%287%2F1%29%2Asqrt%2895%29=highlight%2835sqrt%2895%29%2F4%29=highlight%28about85.3%29 (rounding)

If you were supposed to use trigonometric ratios, the problem did not need to give you both measurements.
Knowing that the central angle (the vertex angle of the 5 triangles measures
360%5Eo%2F5=72%5Eo and the distance from the center to a vertex (7 feet), you could have calculated the length of half of the pentagon's side as
7%2Asin%2872%5Eo%2F2%29=about3.5267 (rounding).
You would have known that the pentagon's side measures approximately 2%2A3.5267ft=7.0534ft or about 7 feet without being told.
Conversely, given the length of a side as 7 feet, you could calculate the distance, h, from the side to the center (in feet) as
h=%287%2F2%29%2Acot%2872%5Eo%2F2%29
You could also have calculated and known (without being told) that the distance from the center to a vertex is about 6 feet, but would not have needed that to solve the problem.