SOLUTION: Solve the following system of equations by using the inverse of the coefficient matrix: x-2y+3z=13 y-z+w=-11 -3x+3y-2z+5w=-6 2y-3z+w=-13

Algebra ->  Matrices-and-determiminant -> SOLUTION: Solve the following system of equations by using the inverse of the coefficient matrix: x-2y+3z=13 y-z+w=-11 -3x+3y-2z+5w=-6 2y-3z+w=-13      Log On


   

Question 732096: Solve the following system of equations by using the inverse of the coefficient matrix:
x-2y+3z=13
y-z+w=-11
-3x+3y-2z+5w=-6
2y-3z+w=-13
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
  x - 2y + 3z      =  13
       y -  z +  w = -11
-3x + 3y - 2z + 5w =  -6
      2y - 3z +  w = -13

 1x - 2y + 3z + 0w =  13
 0x + 1y - 1z + 1w = -11
-3x + 3y - 2z + 5w =  -6
 0x + 2y - 3z + 1w = -13


The cefficient matrix is thi 4x4 matrix:



Find its inverse using a TI-83 or better calculator.
That's this 4x4 matrix



Multiply that by the 4x1 column vector or matrix
from the numbers on the right of the system:

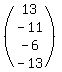
%28matrix%284%2C1%2C%0D%0A13%2C-11%2C-6%2C-13%29%29

%22%22=%22%22%28matrix%284%2C1%2C%0D%0A-9%2C-38%2C-18%2C9%29%29%22%22=%22%22

(x,y,z,w) = (-9,-38,-18,9)
 
Edwin