Question 731943: A 340 meter long train is accelerating from rest at 6 meter/second square. With the start of motion, a man standing at the front end of the train, projects a ball upwards at a velocity of 50 meters/second. Do calculaions to decide if the ball will fall back on the train or will miss it.
Found 3 solutions by lynnlo, ikleyn, KMST:
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by ikleyn(53427)   (Show Source): (Show Source):
Answer by KMST(5330)   (Show Source): (Show Source):
You can put this solution on YOUR website! How does that man "project a ball upwards? How high is the top of the train at the place the ball could hit?
Whatever height the man shoots the ball from let's assume the ball would hit the train at that height or miss the train. Lets say the ball is shot up from the train floor and may fall on the floor of one of some open top cars near the back of the train or miss the train entirely.
THE TEACHER'S SOLUTION:
As the problem says "projects", students should apply
the formula for projectile motion learned in class to describe the ball motion,
and the formula for uniformly accelerated motion to describe the motion of the train.
For a projectile projected up from a height  at an initial speed at an initial speed  , ,
under gravity with an acceleration  , the height as a function of time is , the height as a function of time is

For distance  covered under uniformly accelerated motion during time covered under uniformly accelerated motion during time  with initial speed with initial speed  with a constant acceleration with a constant acceleration  is is

The commonly used value for acceleration of gravity om Earth is
 
With   and and   , using meter and second units, , using meter and second units,
we have  for the ball. for the ball.
Factoring it as  we se that we se that  for for
 and and  = =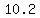 seconds for the ball. seconds for the ball.
For the train, with units of meters and seconds, we have  and and  , ,
so we get the distance covered during while the ball is in the air as
 = = meters. meters.
That is less than the length of the train, so there is still part of the train under the ball as the ball gets down, and hits the train.
THE FIFTH GRADER'S SOLUTION:
The ball starts with an upwards speed of 50meters/second(50m/s), and gravity makes that speed decrease at a rate of 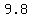 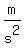 until the upwards speed is zero. until the upwards speed is zero.
After that the ball continues to accelerate downwards at  from the speed of from the speed of 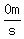 it had at the top of its flight. If nothing stops the ball, it would reach the height level it started from, and at that point its downwards speed would be it had at the top of its flight. If nothing stops the ball, it would reach the height level it started from, and at that point its downwards speed would be 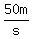 . .
The speed change from 0m/s to 50m/s at a rate of 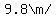 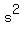 should take should take
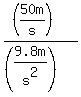  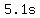
That is the time the ball spent going up to its greatest height.
From there, it would take the same time accelerating from 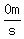 to to 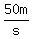 downwards to get to the height it started at the level of the train floor. downwards to get to the height it started at the level of the train floor.
The round trip would have taken  . .
During that time the train has accelerated from 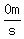 at at  , and has reached a speed of , and has reached a speed of
 (rounded). (rounded).
The distance the train covered during those 10.2 seconds, can be calculated as average speed times 10.2 seconds:
Because the acceleration was constant, the speed increased linearly and the average speed is the average of initial and final speeds for that period of time:
 , and the distance covered during that time period was , and the distance covered during that time period was  (rounded). (rounded).
That mean the front of the train moved that far and as the train's length is 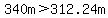 , ,
a spot in the train 312.24 meters behind the front of the train is now where the front of the train was when the ball was projected upwards. The ball will hit the train at that spot.
|
|
|