Question 731622: i have been doing combinations,and i have researched about subsets? and i found out that subsets are 2 to the power n but now i have a question ,given a subset ,how do you find the possible outcomes of choosing a specific number,ie (1,2,3,5,5,6,7,8,9,10,11) ,how many subsets contain the number 5 how many subsets contain exactly three elements, one of which is 3
d. contain exactly five elements, but neither 3 nor
and the question gets complex when it says such,please help
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of subsets with  to to 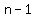 elements from a set with elements from a set with  elements is elements is  elements, there are elements, there are  subsets. subsets.
How many subsets of {1,2,3,4,5,6,7,8,9,10,11} contain the number 5?
One of those subsets will be {5}, with just one element.
If you remove the number 5 from each of the subsets containing 5, you would get all the subsets of {1,2,3,4,6,7,8,9,10,11} and there is 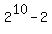 or or  of those (counting the empty set and the whole 10-element {1,2,3,4,6,7,8,9,10,11} set of those (counting the empty set and the whole 10-element {1,2,3,4,6,7,8,9,10,11} set
That is the number of subsets containing 5, counting {5} and {1,2,3,4,5,6,7,8,9,10,11}.
How many subsets of {1,2,3,4,5,6,7,8,9,10,11} contain exactly three elements, one of which is 3?
Removing 3 from each of those subsets would give you all the subsets of {1,2,4,5,6,7,8,9,10,11} with exactly 2 elements and that is  subsets. There are several different combination symbols for that and you know which one you are expected to use. subsets. There are several different combination symbols for that and you know which one you are expected to use.
How many subsets of {1,2,3,4,5,6,7,8,9,10,11} have 5 elements but contain neither 3 not 5?
All of those subsets can be made from {1,2,4,6,7,8,9,10,11} and there is
 of them. of them.
|
|
|