Question 731574: Suppose you deposit $500 in an account with an annual interest rate of 8% compounded monthly.
a. Find an equation that gives the amount of money in the account after t years.
b. Find the amount of money in the account after 5 years.
c. How many years will it take for the account to contain $1000?
d. If the interest were compounded continuously, how much money would the account contain after 5 years?
Thank You So Much!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Interest compounded monthly:
The interest for 1 month would be  of 8%, meaning of 8%, meaning  of the initial balance that month. of the initial balance that month.
So at the end of the first month you would have a balance (in $) of

So the new balance would be the initial balance times 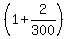 . .
During the second month, you would be earning interest on the whole of that $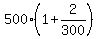 and that balance would be multiplied times and that balance would be multiplied times 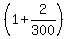 to get the new balance of to get the new balance of

After  months you would have a total of months you would have a total of
$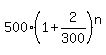
a. At the end of 5 years you would have accumulated interest during  and would have a total of and would have a total of
$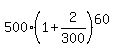 = $ = $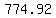 (rounded) (rounded)
b. To get to  you will need you will need  months, and we can find months, and we can find  like this: like this:
From

taking logarithms on both sides, we get
 --> -->  --> --> 
That calculates as about 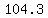 (rounded) (rounded)
If you need $1000, you will have to wait for 105 months because
after 104 months you will have
$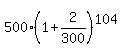 = $ = $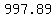 (rounded) (rounded)
but after 105 months you will have
$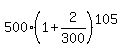 = $ = $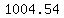 (rounded) (rounded)
c. Interest compounded monthly:
If the interest was calculated and added to the balance after shorter and shorter periods, you would gain a little bit more as the periods were shortened, getting as close as you want, but never going over a certain limit.
That limit is what they call continuous compounding.
The balance with continuous compounding is given by the function
 = $ = $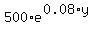 with with  = number of years. = number of years.
In that expression,
$ is the initial deposit, is the initial deposit,
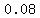 is the 8% interest rate expresed as a decimal, is the 8% interest rate expresed as a decimal,
and  is an irrational number, like is an irrational number, like  . .
For  we get the balance after 5 years as we get the balance after 5 years as
$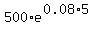 = $ = $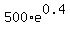 = $ = $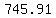
|
|
|