|
Question 730838: Regarding algebfra, polynomials --
Please help me solve this problem. I know the answer is x = 5, but I'm having trouble arriving at the answer correctly.
"The area of a rectangle is 55 square feet. The height is x and the length is 2x + 1. Solve for x."

2x^2 + x = 55
2x^2 + x -55 = 0
My email address is mjj1107@sbcglobal.net.
Thanks.
Mary Jane
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are on the right path and just need to solve 
There are easier quadratic equations
I know of 3 ways to solve quadratic equations like 
Factoring will work if the answers are rational numbers.
Completing the square will always work.
Using the quadratic formula will always work too.
FACTORING:
When the leading coefficient is not 1 or -1, factoring is a little harder.
In this case, you must look for pairs of factors of  . .
Giving a negative sign to one factor and a positive sign to the other, they must add up to the coefficient of the term in x, 1.
The number 110 can be written as 4 different products:




The last one is the one that works because 
So we use 11 and -10 as coefficients of x and write 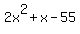 as as
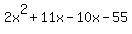
Then we factor by grouping, like this:

So, since  we re-write the equation as we re-write the equation as
 and find the solutions that make and find the solutions that make
 --> -->  and and
 --> --> 
Since x must be positive to be the width of a rectangle, the only solution is  . .
COMPLETING THE SQUARE:
 --> -->  dividing both sides by 2 dividing both sides by 2
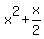 is part of is part of  so if we add so if we add  to both sides we "complete the square: to both sides we "complete the square:
 --> -->  --> -->  --> --> 
 or or  so so
either  --> -->  --> -->  --> --> 
or  --> -->  --> -->  --> --> 
Same solutions to the equation, and the only solution to the geometry problem is  . .
THE QUADRATIC FORMULA
is a formula that derives from completing the square.
I never set to memorize it, but I have been using it for so long that I remember it.
For an equation of the form
 the solutions are given by the quadratic formula: the solutions are given by the quadratic formula:

In the case of   , ,  and and  so so




So the solutions of the equation are
 --> -->  --> -->  --> -->  --> --> 
Since 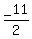 cannot be the with of a rectangle, the only solution is cannot be the with of a rectangle, the only solution is  . .
|
|
|
| |