Question 729916: Solve: cos^2(theta)+ 2sin(theta)=2
Please help. I have no Idea what to do.
Found 3 solutions by stanbon, fcabanski, Leaf W.:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! cos^2(theta)+ 2sin(theta)=2
-----
You have to know cos^2 + sin^2 = 1
----
Your Problem:
(1-sin^2) + 2sin = 2
-----
sin^2 - 2sin + 1 = 0
Factor:
(sin-1)^2 = 0
sin(theta) = 1
theta = pi/2
=================
Cheers,
Stan H.
=================
Answer by fcabanski(1391)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember the identity that  . Whenever there is sin or cos squared and the other not squared, it's a good bet to use that identity. . Whenever there is sin or cos squared and the other not squared, it's a good bet to use that identity.

The equation becomes 
Subtract 2 from both sides.

Multiply each term by negative 1.

Substitute 

That's a quadratic polynomial.
 so x=1 so x=1

Arcsin (1) = 90 degrees. That's only one possible answer, because sin repeats every 2*pi radians (360 degrees). The complete answer is pi + 2*pi*n radians, or 90 + 360n degrees.
Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)
Answer by Leaf W.(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
.
Since  (a fundamental trigonometric identity), you can change this to (a fundamental trigonometric identity), you can change this to  using basic algebra subtraction on both sides and substitute this into your equation for using basic algebra subtraction on both sides and substitute this into your equation for 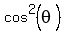 . .
.

.
Move everything to the right side: 
.
Factor: 
.
Solve for  : :  ==> ==> 
.
Now you have to think: for what angles is the sine equal to 1? Well, for  . However, it is also 1 at every complete revolution (every . However, it is also 1 at every complete revolution (every  from from  -- that is, -- that is, 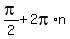 , where "n" is an integer {think , where "n" is an integer {think 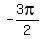 , , 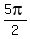 , etc.}). Therefore, the solution to the equation is , etc.}). Therefore, the solution to the equation is  . .
.
IF you have a domain restriction in the problem, only include solutions that are within the domain. For example, if you have a restriction of  , then your solution would be , then your solution would be  only because that is the only solution in only because that is the only solution in 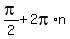 that is between 0 and that is between 0 and  . .
*
I hope this helped! Good luck!
|
|
|