SOLUTION: 10 men can do a piece of work in 24 days. After working 6 days,few men were added to finish the work in 21 days from the begining. Find the added men.

Algebra ->  Rate-of-work-word-problems -> SOLUTION: 10 men can do a piece of work in 24 days. After working 6 days,few men were added to finish the work in 21 days from the begining. Find the added men.      Log On


   

Question 729601: 10 men can do a piece of work in 24 days. After working 6 days,few men were added to finish the work in 21 days from the begining. Find the added men.
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
10 men can do a piece of work in 24 days. After working 6 days, a few men were added to finish the work in 21 days from the begining. Find the added men.
>>...10 men can do a piece of work in 24 days...<<  

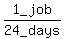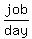So the 10 men's combined working rate is 1_job%2F24_days or 1%2F24job%2Fday.  

Also it would take 1 man 240 days (ten times as long as it would take 10
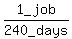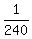
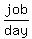men.  So 1 man's working rate is 1_job%2F240_days or 1%2F240job%2Fday.

>>...After working 6 days,...<<
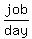In those 6 days the 10 men at the rate of 1%2F24job%2Fday have done
{6/24}}}ths or 1%2F4th of job and so there is still 3%2F4ths of the job
left to be done.

>>...A few men were added to finish the work in 21 days from the begining...<<
Let the number of men added be N.  So for the remaining 21-6 or 15 days,
we have 10+N men working at the combined rate of (10+N)·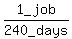1_job%2F240_days
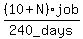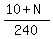
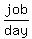or %2810%2BN%29job%2F240_days or %2810%2BN%29%2F240job%2Fday doing 3%2F4ths of the job.
 
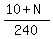
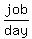So 15 days times their %2810%2BN%29%2F240job%2Fday rate should equal 3%2F4ths of the job.

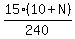
                               15%2810%2BN%29%2F240%22%22=%22%223%2F4

Cross multiply:

                                 60(10+N) = 3·240
                                 60 + 60N = 720
                                      60N = 660
                                        N = 11 

So they added 11 men.

Edwin