Question 729545: at what speed would a car be traveling if it hit a parked car head on without applying the breaks and drove the parked car back 30'
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve the problem using math (and physics) we would have to assume a model. Unfortunately, for complex situations like that, models are far from perfect, and calculated results may not agree well with real world results. On top of that, there are a lot of necessary assumptions that may be wrong.
If we assume that the moving car is not being pushed forward by its engine or pushed back by its brakes, we would conclude that it will be slowed down only by the friction on the tires of the parked car.
Physics textbooks tell us that friction always opposes the direction of movement, and is proportional to (varies directly with) the force pressing together the sliding surfaces. They may say that the coefficient of friction between rubber and dry cement is 0.7. (Values given vary). A somewhat stronger force is supposed to hold surfaces together when they are not sliding across each other, but in the case of the hit car, that force is going to be operating for only a tiny fraction of a second.
If the cars move together as a unit after the collision, we assume the force of friction will be constant and will decelerate the cars at a constant rate until they stop, so the initial velocity  would be related to time (in seconds) until it stops would be related to time (in seconds) until it stops  and negative acceleration and negative acceleration  by the equation by the equation

If the road is level, the force pressing the tires of the parked car is 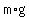 where where  is the mass of the parked car, and is the mass of the parked car, and  is the acceleration of gravity. is the acceleration of gravity.
Assuming a dry cement road, an using feet and seconds as length and time units, frictional force would be calculated as 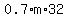 . .
If that force acts on both cars moving as a unit and the moving car has the same mass, the total mass would be 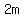 , and the acceleration would be , and the acceleration would be

The distance traveled during a period of  seconds by an object under constant acceleration with zero velocity at the beginning or end can be calculated as seconds by an object under constant acceleration with zero velocity at the beginning or end can be calculated as
 <--> <-->  and multiplying both sides times and multiplying both sides times  we get we get

As  , ,  can be substituted to get can be substituted to get  --> --> 
Using  and and  we get we get 

So the calculated velocity of the moving car is 18 miles per hour.
|
|
|