|
Question 72952: Find the exact solution to the equation 3^x+5 = 9^x.
HELP Pleeze
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Interesting problem.
.
Given:
.
 Find x. Find x.
.
Recognize that 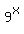 is equal to is equal to 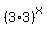 which in turn is equal to which in turn is equal to 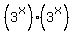
and this is equal to 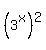 . Lots of practice using the power rule for exponents . Lots of practice using the power rule for exponents
in that little exercise. Anyway, substitute 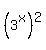 for for 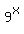 in the original in the original
equation you were given. When you do the equation becomes:
.

.
Off to the races! So we can find it a little easier to see what's going on, let's define
z as being equal to 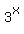 . Go through the equation and substitute z everywhere . Go through the equation and substitute z everywhere
you see 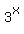 . When you do that the equation becomes: . When you do that the equation becomes:
.

.
Subtract  from both sides of the equation to get: from both sides of the equation to get:
.

.
Then multiply the whole thing by -1 to get the standard quadratic form of:
.

.
Compare this to the standard quadratic form of  and you see that and you see that
a = 1, b = -1, and c = -5. Substitute these values into a solution for the quadratic form
which is (since we are actually solving for z):
.

.
substitute the values for a, b, and c to get:
.

.
this simplifies to:
.

.
the extreme right side of this equation is just a number you can whip out on a calculator.
You need to check this but I got  . .
.
But now we need to go back to our definition for z. We said that  and we can and we can
substitute that for z to get 
.
Let's solve this by taking the log of both sides:
.

.
By the rules of logs, the exponent on the left side becomes the multiplier of the log and
the equation becomes:
.

.
Solve for x by dividing both sides of this equation by log(3) to arrive at:
.

.
The right side of this can be done on a calculator. I got 
.
If you go back to the original problem and substitute this value for x, you should find
that the left side of the equation  equals the right side of the equation equals the right side of the equation
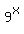 . Use a calculator to do this ... obviously. . Use a calculator to do this ... obviously.
.
Sound OK??? Not so fast. Remember way back when we used the quadratic formula to solve
for z. We only looked at the value of z when there was a plus sign between the 
and the  . There is another solution for z when you put a minus . There is another solution for z when you put a minus
sign between these two terms. This second solution is  . .
.
Again replace z by 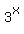 and you get and you get  . As we did previously, . As we did previously,
take the log of both sides and you will end up with 
.
But if you try to take the log of the negative number in the numerator you will get an error
indication. Logs of negative numbers don't work. So we can discard this as a possible answer.
.
The answer to your problem x = 0.934363372.
.
Wow! Lots of fun with this one. Time for another Pepsi.
.
Hope this helps you. Since this was a pretty complex problem, I figured you had a math
background with logs and exponents. I sure hope that you were able to track what I did here.
Good luck ...
|
|
|
| |