Question 729502: I have a question about quadratic equation. I know if you need to square a negative number then it will be that number with an I at the end but we haven't learned that yet so I'm not sure if I'm doing the problem right. Here's what I'm doing:
4x^2-6x+2=0
6 plus or minus square root of (-6^2-4(4)(2)over 2(4)
6 plus or minus square root of (-36-72) over 8
6 plus of minus square root of (-108) over 8
Can you tell me what I am doing wrong? Or would the problem be considered non solvable?
Found 2 solutions by ankor@dixie-net.com, KMST:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 4x^2-6x+2=0
This equation can be factored
Factor out 2 first
2(2x^2 - 3x + 1) = 0
Factor what's left
(2x - 1)(x - 1) = 0
Two solutions
2x = 1
x = 1/2
and
x = 1
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You tried to use
 , ,
the quadratic formula.
That cumbersome formula always works, but I only use it if I have to.
When you apply it properly, you get
 , which simplifies to , which simplifies to

You had two errors:
 Products of two negative numbers are positive, so all squares are always positive Products of two negative numbers are positive, so all squares are always positive
 I really do not know where your 72 came from. I really do not know where your 72 came from.
So,
 --> -->  --> --> 
That gives you solutions
 and and  . .
NOTES:
Alternate ways to solve the problem are factoring, and completing the square.
You could have chosen to simplify the problem first and solve it by factoring, as ankor showed you better than what I was typing.
Factoring does not always work, and completing the square is not always easy.
However, the alternate ways do not require to memorize a formula, and sometimes they are much easier than applying the quadratic formula.
Factoring:
I had typed my wordy explanation, but ankor did it better.
Completing the square:
 shares all the same terms in x as shares all the same terms in x as 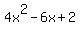
 --> --> 
Adding  to both sides of the equal sign, we get a "completed" square on the left side: to both sides of the equal sign, we get a "completed" square on the left side:
 --> -->  --> --> 
Since  and and  it could be that it could be that
 or that or that  and each of those equations leads us to a solution. and each of those equations leads us to a solution.
|
|
|