Question 72900: determine the type of solution considering only its discriminant
x^2-9=0
4x^2+16x=0
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! First Problem:
.
Given 
.
Comparing this form to the standard quadratic form of
.

.
you can see that a = 1, b = 0, and c = -9
.
The discriminant is given by the equation:
.
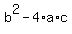
.
Substitute into this expression the values for a, b, and c as noted above and you get:
.
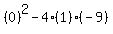
.
Do the algebra and you get:
.

.
Since the discriminant is a positive value you know that the type of solution leads to
two real, but unequal values for x.
.
[Note that this quadratic factors easily to  which by setting each which by setting each
factor equal to zero tells you that the two solutions are  and and  ] ]
.
Second problem:
.
Given: 
.
Comparing this equation to the standard form of the quadratic equation you can determine that
a = 4, b = 16, and c = 0
.
Substituting these values into the discriminant 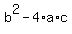 results in: results in:
.

.
This reduces to:
.

.
Since the discriminant is positive, you again can say that the solutions for x are real,
and unequal.
.
In fact, you might have noticed that x can be factored from the given expression for this
problem. Therefore, x = 0 is one of the two solutions.
.
Hope this helps you to understand the value of the discriminant in finding characteristics
of the answers to quadratic equations that are in standard form.
|
|
|