SOLUTION: Write as a single logarithm {{{3logx-(1/2)log(x-2)+2log(x+5)^3}}} PLZ help I need tis as soon as possible

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Write as a single logarithm {{{3logx-(1/2)log(x-2)+2log(x+5)^3}}} PLZ help I need tis as soon as possible       Log On


   

Question 72874: Write as a single logarithm
3logx-%281%2F2%29log%28x-2%29%2B2log%28x%2B5%29%5E3
PLZ help I need tis as soon as possible
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
3logx-(1/2)log(x-2)+2log(x+5)^3
=logx^3 - log(x-2)^(1/2) + log(x+5)^2
=log[(x^3)(x+5)^2/(x-2)^(1/2)]
Cheers,
Stan H.

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
We're going to use these identities to rewrite the problem
1. ylog%28x%29=log%28x%29%5EyAny number multiplied by a log can be placed as an exponent over the log's argument
2. log%28x%29-log%28y%29=log%28x%2Fy%29The difference of two logs (with the same base) is equivalent to the log with 2 arguments divided.
3. log%28x%29%2Blog%28y%29=log%28x%2Ay%29The sum of two logs (with the same base) is equivalent to the log with 2 arguments multiplied.


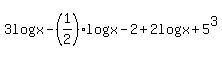3logx-%281%2F2%29log%28x-2%29%2B2log%28x%2B5%29%5E3Start with given problem.
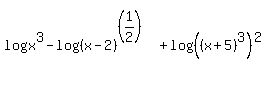log%28x%29%5E3-log%28%28x-2%29%29%5E%28%281%2F2%29%29%2Blog%28%28%28x%2B5%29%5E3%29%29%5E2Rewrite using identity 1. Place all numbers multiplying by the logs as exponents over their arguments.
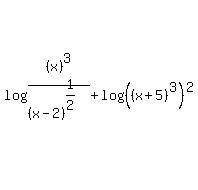log%28%28x%29%5E3%2F%28x-2%29%5E%281%2F2%29%29%2Blog%28%28%28x%2B5%29%5E3%29%29%5E2Rewrite using identity 2. The second log is being subtracted from the first, so rewrite those two that makes the 1st number as the numerator and the 2nd as the denominator.
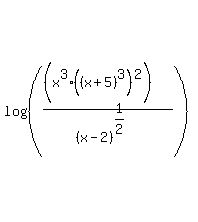log%28%28%28%28x%5E3%2A%28%28x%2B5%29%5E3%29%5E2%29%29%2F%28x-2%29%5E%281%2F2%29%29%29%29 Rewrite using identity 3. Finish it up by multiplying the arguments of the logs that are being added.


This may seem like a lot if you've never seen these identities before, so feel free to ask further why I did a certain step. Hope this helps.