>>...A machine caps a 1000 bottles in 10 minutes,...<<
So the slower machine's bottle capping rate is 1000 bottles
per 10 minutes or
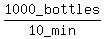 =
= 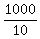
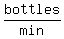 = 100
= 100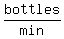
another machine caps 1000 bottles in 8 minutes.
So the faster machine's bottle capping rate is 1000 bottles
per 8 minutes or
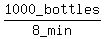 =
= 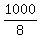
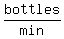 = 125
= 125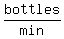
>>...If these machines were together how much time will it take to cap 1000 bottles?...<<
Let that time be x minutes
So their combined bottle capping rate is 1000 bottles
per x minutes or
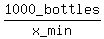 =
= 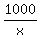
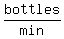 The equation comes from:
The equation comes from:




 100
100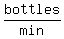 + 125
+ 125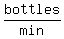

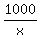 100 + 125 =
100 + 125 = 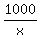 225 =
225 = 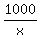 225x = 1000
x =
225x = 1000
x = 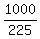 x =
x =  minutes
----------------------------------------------------------------
minutes
----------------------------------------------------------------
b) if t1 and t2 are the time in the above problem. Determine the time taken by both machines working together?
>>...A machine caps a 1000 bottles in t1 minutes,...<<
So the slower machine's bottle capping rate is 1000 bottles
per t1 minutes or
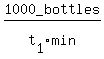 =
= 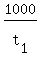
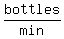
>>...another machine caps 1000 bottles in t2 minutes...<<
So the faster machine's bottle capping rate is 1000 bottles
per t2 minutes or
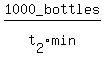 =
= 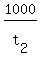
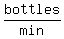
>>...If these machines were together how much time will it take to cap 1000 bottles?...<<
Let that time be x minutes
So their combined bottle capping rate is 1000 bottles
per x minutes or
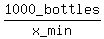 =
= 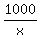
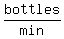 The equation comes from:
The equation comes from:





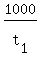
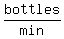 +
+ 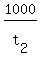
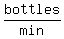 =
= 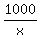
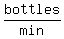
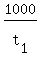 +
+ 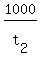 =
= 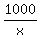 The LCD is t1t2x
1000t2x + 1000t1x = 1000t1t2
Divide through by 1000
t2x + t1x = t1t2
Factor out x on left
x(t2 + t1) = t1t2
Divide both sides by (t2 + t1)
The LCD is t1t2x
1000t2x + 1000t1x = 1000t1t2
Divide through by 1000
t2x + t1x = t1t2
Factor out x on left
x(t2 + t1) = t1t2
Divide both sides by (t2 + t1)
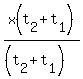 =
= 
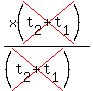 =
=  x =
x = 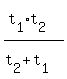 minutes
That's the answer.
-------------------------------------------------------------------------
So the formula is "the product of the times over the sum of the times":
We could have used that formula to solve (a) if we had had it, with
t1 = 10 and t2 = 8
x =
minutes
That's the answer.
-------------------------------------------------------------------------
So the formula is "the product of the times over the sum of the times":
We could have used that formula to solve (a) if we had had it, with
t1 = 10 and t2 = 8
x = 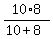 x =
x = 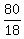 x =
x =  x =
x = 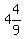 minutes
Edwin
minutes
Edwin