Question 728358: A man 2m tall walks horizontally at a constant rate of 1 m/s toward the base of a tower 25m tall. When the man is 10m from the tower, how fast is the angle of elevation changing if that angle is measured from the horizontal to the line joining the top of the man's head to the top of the tower?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve this problem in a strictly accurate way requires calculus, because the rate of change of the angle is not constant.
We could an expression for the angle as a function of time, calculate the derivative of that function, and then calculate the value of that derivative at the time the man is 10m from the tower.
Alternatively we could obtain an approximate value by calculating the average rate of changeover short period(s) of time at around that time.
APPROXIMATE SOLUTION:
If  = angle of elevation = angle of elevation
when the man is 10 meters from the base of the tower,
 because the horizontal from the top of the 2 meter tall man's head passes by a point 2 meters above the base of the tower and because the horizontal from the top of the 2 meter tall man's head passes by a point 2 meters above the base of the tower and
 below the top of the tower below the top of the tower
(assuming the ground is horizontal between the man and the tower).
When the man is 11 meters from the base of the tower,
 , and , and
when the man is 9 meters from the base of the tower,

Approximate calculations of tangents and the corresponding angles in radians:
 --> --> 
 --> --> 
The average rate of change of that angle of elevation over the second the man shortens his distance from the foot of the tower from 10m to 9m , in radians per second, is

In degrees per second, it would be approximately  . .
 --> --> 
The average rate of change of that angle of elevation over the second the man shortens his distance from the foot of the tower from 11m to 10m , in radians per second, is

In degrees per second, it would be approximately 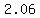 . .
The instantaneous rate of change at thye precise time when the man is 10 meters from the base of the tower must be somewhere in between, but maybe  per second is accurate enough for an answer. per second is accurate enough for an answer.
Otherwise, we could average the results an come up with
 radians per second = about radians per second = about  per second per second
WITH CALCULUS:
 = time until the man reaches the bottom of the tower, in seconds. = time until the man reaches the bottom of the tower, in seconds.
so  = horizontal distance between the man and the tower in meters = horizontal distance between the man and the tower in meters

 = =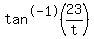
Since the derivative of  is is  , ,
the rate of change of 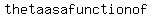 is is

That rate of change is negative, of course, because as the time needed to reach the foot of the tower increases, the angle decreases.
We are interested in the opposite because we are decreasing the time needed to reach the foot of the tower.
The rate of increase of the angle as the man approaches the tower, as a function
of time is

When  that rate is exactly that rate is exactly  radians per second, with units of radians per second, with units of  . .
In the more familiar degrees per second, the numerical value would be exactly
 . .
|
|
|