Question 72786This question is from textbook Essential Algebra
: (-5w^2x^3y)(-wxz^3)(3vxy^2)(-4wz^3) Simplify.
This question is from textbook Essential Algebra
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Simplify:
.

.
Until you get a little more experience, let's do some things that will make it more difficult
to make a mistake.
.
In the term inside the second set of parentheses let's insert a multiplier of 1 so the term
becomes 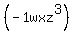
.
Let's go through all the terms and wherever we see a letter without an exponent, let's give
that letter an exponent of 1.
.
These two changes modify the expression so it now reads:
.
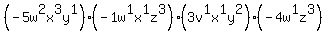
.
One final thing ... let's identify all the variables to make sure we don't miss any. List them
in alphabetical order. The variables are: v, w, x, y, and z
.
Now let's attack the problem.
.
First multiply the numbers in front of all the terms. Make sure you keep them associated
with their correct sign. For this multiplication you should get:
.

.
Now in order, go through all the variables, one at a time, and add their exponents.
.
v first. Adding the exponents of the letter v gives you an answer of 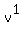 because the letter because the letter
v appears only once and its exponent is 1. Write it as just  instead of instead of 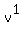 . .
.
w second. Adding the exponents for w results in  so multiplication of so multiplication of
the w terms ends up as 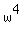 . .
.
x next. Adding the exponents of x results in  so the multiplication of so the multiplication of
the x terms gives 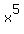 as the answer. as the answer.
.
y next. Adding the of y results in  . So multiplication of the y terms gives . So multiplication of the y terms gives
you an answer of  . .
.
Finally z terms ... add the exponents of z  indicating that the product of indicating that the product of
the z terms results in 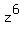
.
As a check add up all the exponents of our answers.  . Then go back to . Then go back to
the original problem and add up all the exponents that appear in the problem. 
The count agrees so we probably did not make an error.
.
Now multiply all our answers together to get:
.
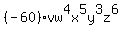
.
That's the answer.
.
Hope this helps you to understand the problem. Once you get used to it, you'll be able to
eliminate some of the steps such as inserting exponents of 1 to make sure you don't miscount.
|
|
|