xy(x² + y²) = 300
x² + xy + y² = 37
There is an x² + y² in both equations.
Isolate x² + y² on the left of both equations:
x² + y² =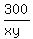 
x² + y² = 37 - xy
Equate the right sides:
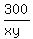= 37 - xy
Multiply through by xy
300 = 37xy - (xy)²
(xy)² - 37xy + 300 = 0
That is a quadratic in xy and it factors as
(xy - 25)(xy - 12) = 0
xy - 25 - 0; xy - 12 = 0
xy = 25; xy = 12
Solve each for y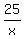
y = 
; y = 
Substitute in the first equation:
xy(x² + y²) = 300; xy(x² + y²) = 300
25(x² +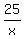²) = 300; 12(x² +²) = 300
x² +
= 12; x² +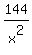
= 25
x4 + 625 = 12x² x4 + 144 = 25x²
x4 - 12x + 625 = 0 x4 - 25x² + 144 = 0
This equation has imaginary
solutions, (x² - 16)(x² - 9) = 0
which are too much trouble x² - 16 = 0; x² - 9 = 0
to find, so I'll just stick (x - 4)(x + 4) = 0; (x - 3)(x + 3) = 0
with the real solutions only. x - 4 = 0; x + 4 = 0; x - 3 = 0; x + 3 = 0
x = 4; x = -4; x = 3; x = -3
Substituting each of those in y = ,
y = 3; y = -3; y = 4; y = -4
So the real solutions are
(x,y) = (4,3), (x,y) = (-4,-3), (x,y) = (3,4), (x,y) = (-3,-4)
There are four more imaginary solutions coming from the
equation: x4 - 12x + 625 = 0
which involve square roots or expressions that involve
square roots. It's too much trouble to find those
exactly, so I'll just do the 4 real solutions, and only
approximate the 4 imaginary solutions with a calculator.
x = 3.937 + 3.082i, y = 3.937 + 3.082i
x = 3.937 - 3.082i, y = 3.937 + 3.082i
x = -3.937 + 3.082i, y = -3.937 - 3.082i
x = -3.937 - 3.082i, y = -3.937 + 3.082i
Edwin
