I'm assuming you want to distribute the w right? Well if you do, you will want to multiply w by every term inside the parenthesis.
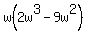Start with given expression
Distribute the w. This means that the w is multiplied by 2w^3 and 9w^2
Simplify the expression. When multiplying 2 variables with exponents you add the exponents (for example 
)
If that didn't make any sense, or you just are having a hard time understanding distribution, make a simpler problem. For instance try looking at
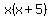
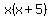Distribute the x among x and 5
Simplify
To help even further, lets put some numbers into this expression. Let x=2
place x=2 into each x
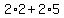
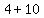
It turns out that if we add the values inside the parenthesis and then multiply, we will get the same answer
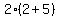
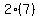
Which shows that 
is true. The reason why we have to distribute in this problem is because we don't know what w is. w could be anything, so we cannot add it to a known value (there's no way to do it). So we distribute the w to simplify the problem, and since there are no further instructions, we'll leave it at
Hope this helps. Throughout this problem, I'm assuming that distribution is giving you trouble and I hope I'm correct.
(