|
Question 727341: Hello! I'm having a bit of difficulty with one of my homework problems. Here it is:
Working together it takes Larry, Moe and Curly 3 hours to paint a room. If Curly takes twice as long as Larry, and Moe takes one hour more than Larry, how long would it take Larry to paint the room by himself?
So far I have:
Larry: 1/x
Moe: 1/x+1
Curly: 1/2x
And if it's anything like previous work-rate problems, I'm assuming you set it up as:
1/x + 1/x+1 + 1/2x = 3
What do I do next? Am I somehow supposed to make the denominators the same?
I know I'm supposed to eventually get to a quadratic equation, but if anyone has the next step or sees something I'm doing incorrectly, I'd love some input!
Thank you very much!
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your method mishandles Moe and Curly work rates and data. Only the assigning of 1/x to Larry made sense. At least you began to see "jobs per unit of time" as the work rate.
Using your x for the time needed for Larry to do one job, we can create expressions for their work rates as jobs per time (hours).
Rates of work for each worker:
Larry, 1/x jobs per hour, meaning 1 job in x hours.
Moe, 1/(x+1), meaning 1 hour more than Larry to do the job alone.
Curly, 1/(2x), meaning 1 job needing twice the time as for Larry.
Note that I use parentheses to eliminate any confusion about the numbers or variables being divisors or factors.
Those same rates using this site's rendering:
Larry, 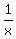 jobs per hour jobs per hour
Curley,  jobs per hour jobs per hour
Moe,  jobs per hour, (site was failing to display during writing time.) jobs per hour, (site was failing to display during writing time.)
We sum their rates when they all work together. They do the job as a group in 3 hours, so our sum is:
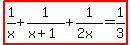
That is, together, they work at the rate of ONE job per THREE HOURS.
Just be sure you understand the development of that equation for sum of the rates. The actual Algebra steps should be mostly mechanical process of steps from there.
|
|
|
| |