SOLUTION: Joey saved $2 today. If he doubles the number of dollars he saves each day, how many days, including today, will it take him to save more than $500?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Joey saved $2 today. If he doubles the number of dollars he saves each day, how many days, including today, will it take him to save more than $500?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 726849: Joey saved $2 today. If he doubles the number of dollars he saves each day, how many days, including today, will it take him to save more than $500?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
This is a geometric sequence with a factor of 2: 2, 4, 8, 16...


The sum of a geometric series is 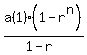a%281%29%2A+%281-r%5En%29%2F%281-r%29 where a(1) is the first term, r is the common factor, and n is the nth term (the number of the term that = the sum). Set this = 500 and solve for n. The n needed (the numbered term) will be greater than that n.


a(1) = 2 and r=2. The desired sum is 500.
500+=+2%2A%281-2%5En%29%2F%281-2%29+


-500+=+2%281-2%5En%29


-250+=+1-2%5En


2%5En+=+251


Recall that x%5En=y when log (base x)y = n so log(base 2) 251 = n = approx. 7.97


Therefore the sum of the first 7.97 terms is 500, so the sum exceeds 500 with the 8th term or 8th day.


You could have also solved this by writing out the amount he saved each day, and adding: 2, 4, 8, 16, 32, 64, 128, 256 (the sum is $510, which exceeds $500 on the 8th day.)

Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)