Question 726739: A right rectangular prism with dimensions 2/3in. by 4/3in. by 8/3in. is enlarged by a scale factor of 1 1/2.
Q: The surface area of the original prism is ___ times as much as the surface area of the larger right rectangular prism.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Such an evil problem! It's trying to trick us two ways.
The shoebox-like prism has a length, L, a width, W, and a height, H, that are all fractional quantities of inches.
However, those numbers do not matter, given the question at the end.
When you enlarge dimensions by a factor of  , ,
the surface area of a solid changes by a factor of  and the volume by a factor of and the volume by a factor of  . .
That happens because you have to multiply pairs of dimensions to get surface area, so when you multiply each pair, you get an  as a factor. as a factor.
A face that had an area of  gets it changed to gets it changed to  . .
A face that had an area of  gets it changed to gets it changed to  . .
A face that had an area of 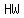 gets it changed to gets it changed to  . .
The scale factor was 
The dimensions of the large prism are  of the dimensions of the small one. of the dimensions of the small one.
The dimensions of the small prism are  = =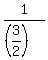 of the dimensions of the large one. of the dimensions of the large one.

The surface area of the original (smaller) prism is  times as much as the surface area of the larger right rectangular prism. times as much as the surface area of the larger right rectangular prism.
|
|
|