SOLUTION: The cost of producing 20 cakes is $315, while 35 cakes is $495. (a)Find the linear cost equation (b)What is the y-intercept and interpret the answer? (c)What is the gradient

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The cost of producing 20 cakes is $315, while 35 cakes is $495. (a)Find the linear cost equation (b)What is the y-intercept and interpret the answer? (c)What is the gradient      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 726707: The cost of producing 20 cakes is $315, while 35 cakes is $495.
(a)Find the linear cost equation
(b)What is the y-intercept and interpret the answer?
(c)What is the gradient and interpret the answer?
(d)Find the cost of producing 55 cakes
(e)How many cakes can be produced with $1000.
This was a practice question from a revision test for an exam. If you could, could you please answer this question ASAP, as my exam is in a couple of days. This would be greatly appreciated. Thank you very much :)
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
The cost of producing 20 cakes is $315, while 35 cakes is $495. 
Let x = the number of cakes produced
Let y = the cost of preparing those x cakes.

The cost of producing 20 cakes is $315,
When x = 20, y = 315, indicated by the ordered pair (20,315)

while 35 cakes is $495
When x = 35, y = 495, indicated by the ordered pair (35,495)

(a)Find the linear cost equation
That is the same as the equation of the line that goes through
the points (20,315) and (35,495)

We use the slope (gradient) formula:

m = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (20,315)
and where (x2,y2) = (35,495)

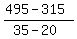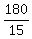m = %28495-315%29%2F%2835-20%29 = 180%2F15 = 12

Then we use the point-slope (or point-gradient) formula:

y - y1 = m(x - x1)

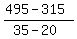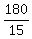m = %28495-315%29%2F%2835-20%29 = 180%2F15 = 12

y - 315 = 12(x - 20)

y - 315 = 12x - 240

      y = 12x + 75

(b)What is the y-intercept and interpret the answer?
The y intercept is when x = 0

      y = 12x + 75
      y = 12(0) + 75
      y = 0 + 75
      y = 75

So the y-intercept is (0,75).  That means that when
no (x=0) cakes have yet been produced, the fixed costs are 
$75, just for setting up and going into the business
of producing cakes.

(c)What is the gradient and interpret the answer?
The slope or gradient is m=12.  That means that the cost
per cake increases by $12 per cake.

(d)Find the cost of producing 55 cakes
We substitute x=55 into 

      y = 12x + 75
      y = 12(55) + 75
      y = 660 + 75
      y = 735

Answer: $735

(e)How many cakes can be produced with $1000.
We substitute y = 1000 in

      y = 12x + 75

and solve for x:

   1000 = 12x + 75
    925 = 12x 
 77.083 = x, round down to 77.

Answer:  77 cakes can be produced for $1000    

Edwin