SOLUTION: Okay, got 3 problems that are giving me problems! All 3 involve maximizing and minimizing. I know the answers, I just don't know how to do the work. I must show it algebraically, n

Click here to see ALL problems on Miscellaneous Word Problems

Question 725967: Okay, got 3 problems that are giving me problems! All 3 involve maximizing and minimizing. I know the answers, I just don't know how to do the work. I must show it algebraically, not just by guessing. Please help me with set up!!
1) What is the maximum product of two numbers that have a sum of 26? (I know the answer is 169, 13x13, but how do I show this by solving an equation?)
2) What is the minimum product of two numbers that differ by 8? What are the numbers?
3)A rectangular compost container is to be formed in a corner of a fenced yard, with 8ft. of chicken wire completing the other two sides of the rectangle. If the chicken wire is 3 ft. high, what dimensions of the base will maximize the container's volume?
Thanks in advance!
Found 2 solutions by richwmiller, fcabanski:
Answer by richwmiller(17219) (Show Source):
You can put this solution on YOUR website!
2) there is no minimum since both numbers can be negative.

Answer by fcabanski(1391) (Show Source):
You can put this solution on YOUR website!
1. x+y=26 thus y = 26-x. Maximize x*y, which is the same as x(26-x) = 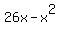That's a parabola. You can use calculus to find the maximum, or you can find the x-coordinate of the vertex of the parabola = -b/2a where a is the coefficient of the squared term and b is the coefficient of the variable term.

a=-1, b=26 so -b/2a = -(26/-2) = 13.

When x=13 y= 26-13=13. The numbers are 13 and 13.

Using calculus set the derivative - 0. 26-2x = 0 ---> -2x = -26 ---> x = 13.

2. y=x+8. Minimize xy, which is minimize x(x+8) = .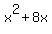

a=1, b=8. -b/2a = -8/2 = -4. y = -4+8=4. The numbers are 4 and -4.

Using calculus set 2x+8=0---> 2x=-8--->x=-4. y=-4+8 = 4.

3. Volume is length*width*height. Call length x and width y. The height is 3. So maximize x*y*3 when x+y=8 or y=8-x.

x*(8-x)*3 =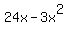

a=-3 and b=24. The x-coordinate of the vertex is -(24/-6) = 4.

y=8-4 = 4. 4x4 maximizes the volume.

Using calculus set 24-6x=0 --->-6x=-24 --->x=4 and y=8-4=x.

Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)