Question 725493: Moe, Curly, and Larry are to mow a rectangular lawn that measures 100 feet by 120 feet. Moe is going to mow one-third of the lawn by mowing a strip of uniform width around the outer edge of the lawn. What are the dimensions of the lawn still to be mowed?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the width of sidewalk be x
..
Length of garden 120 feet
width of garden 100 feet
Area = 12000 m^2
Area of sidewalk 4000 m^2
length of garden & sidewalk 120 + 2 x
width of garden & sidewalk 100 + 2 x
( 120 + 2 x ) ( 100 + 2 x ) + -12,000 = 4,000
12,000 + 240 x + 200 x + 4 X^2 + -12,000 = 4,000
4 X^2 + 440 x + -4,000 = 0
Find the roots of the equation by quadratic formula
a= 4 b= 440 c= -4,000
b^2-4ac= 193,600 - -64,000
b^2-4ac= 257,600 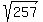 = 508 = 508


x1=( -440 + 508 )/ 8
x1= 8
x2=( -440 -508 ) / 8
x2= -16
Ignore negative value
width of sidewalk = 8 feet
dimensions of lawn to be mown .
length 120-16=104 ft
width = 100-16=84 ft
|
|
|