|
Question 724892: I need help with this rational expression: (5+x/2x^2) + (2/3x) = (1/3)
This is what I have tried so far: First I made all od the bottom part of the fraction the same, and I got this, (15x+3x^2=4x^2)/(3x)(2x^2) = (-2x^3)/(3x)(2x^2) then i combined like terms and got 7x^2+15x=-2x^3 I don't know what to do after that or know if it is right. Please help!! I greatly appreciate it.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
For several reasons you have made this problem much harder than it needed to be:- If this had been an "rational expression" then you would need to do exactly what you did: get the common denominators and add the terms. But this is not a rational expression. It is a rational equation. And as an equation we have a much easier path: Eliminate the fractions by multiplying both sides of the equation by the lowest common denominator (LCD). (I will show you this later.)
- You did not use the LCD. You used a common denominator, not the lowest. Anytime you use a common denominator that is not the lowest you make the rest of the problem harder.
- Where did the "-" on the right side come from? This is only "fatal" error you made. The previously mentioned items just made the problem harder. This one makes it impossible to get the right answer.
I'm going to address all three of these items... in reverse order.
3. Correcting the error.

To solve an equation like this, with powers of x greater than 1, we want one side to be zero and to factor the other side. Since factoring is easier with a positive leading coefficient, the "2" in front of x cubed, I am going to subtract the entire left side from both sides:

Now we factor. First the greatest common factor (GCF). The GCF is x:

And now the trinomial:

From the Zero Product Property:
x = 0 or 2x+3 = 0 or x-5 = 0
Solving these we get:
x = 0 or x = -3/2 or x = 5
Last, we check. This is required when solving rational equations because you must ensure that no denominator becomes a zero. Use the original equation to check:

Checking x = 0:

We can already see that not just one but two denominators will be zero. So we must reject this solution.
Checking x = -3/2:

We can already see that no denominators will be zero. So there is no reason to reject this solution. (You're welcome to finish the check to see if -3/2 actually works (IOW: to see if we've made a mistake).
Checking x = 5:

We can already see that no denominators will be zero. So there is no reason to reject this solution. (You're welcome to finish the check to see if 5 actually works (IOW: to see if we've made a mistake).
2. The LCD.
If you have trouble identifying the LCD, then I have found that a certain technique can be very helpful. First you fully factor the denominators. By "fully" I mean factor numbers into prime factors and rewrite any variables with exponents without the exponents. (I'm going to include all three denominators a) to show you how this works with more than two and b) to use in solving the equation in the easiest way (#1))
2x^2 = 1 * 2 * x * x
3x = 1 * x * 3
3 = 1 * 3
LCD = 1 * 2 * x * x * 3 = 6x^2
Note:- The first lines are the denominators and their fully factored forms. The last line is the LCD.
- Notice how spacing and rearranging the order have been used to ensure that each column has the same factor. This is critical to this technique!
- The LCD is uses one factor from each column.
- The 1's are not really necessary for finding LCD's. This technique can also be used to find GCF's, too, and for those the 1's can be important. (I'll show you finding GCF's at the end.) So as a matter of habit I just always include the 1's.
Not only does this technique help us find the LCD, it can also help us know what to multiply each fraction by to turn its denominator into the LCD. For example, for the fraction
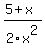 we compare the 2x^2 and LCD lines from the table above: we compare the 2x^2 and LCD lines from the table above:
2x^2 = 1 * 2 * x * x
LCD = 1 * 2 * x * x * 3
We can see that the only thing "missing" from the 2x^2 line is a 3. So we would multiply the numerator and denominator by 3:

For the fraction 1/3 we compare the lines for 3 and the LCD:
3 = 1 * 3
LCD = 1 * 2 * x * x * 3
We can see that the line for 3 is "missing" factors of 2, x and a second x. So we multiply 1/3 by 2x^2/2x^2.
I'll leave it up to you if you want to re-do the problem using the LCD (6x^2) instead of what you used (6x^3). You will find that the factoring is easier and you might not end up with a solution you have to reject (like x = 0).
1. The fast way.
You find the LCD of all the denominators on both sides of the equation (which we have done above). Then you multiply each side of the equation by the LCD:

On the left side we need to use the Distributive Property:

If we have correctly found the LCD, then every denominator will cancel with part or all of the LCD:

which simplifies as follows:


Then we get one side equal to zero, factor and then use the Zero Product Property like we did earlier (except we don't get a solution we have to end up rejecting).
P.S. To use the factoring technique above to find a GCF you do the same thing except the GCF only uses factors from columns that are "full". IOW: from columns that have no blank spaces in them. For example, to find the GCF of the three denominators we would write:
2x^2 = 1 * 2 * x * x
3x = 1 * x * 3
3 = 1 * 3
GCF = 1
The only column that is full is the 1's column. So the GCF 0f 2x^2, 3x an 3 is 1.
|
|
|
| |