SOLUTION: i need the proof of law of cosines and sines

There are three cases for the law of cosines and 2 cases for
the law of sines:

Case 1:
a² = b²+c²-2·b·c·cos(A)  when ∠A and ∠B are both acute angles.


Draw altitude CD ⊥ AB.  Label CD h for the height of ߡABC.
Label the left part of c, AD as x and the right part of c DB as c-x.


 
ߡADC and ߡBDC are right triangles, so by the Pythagorean
theorem,

h² = b²-x² and also h² = a²-(c-x)²

Therefore equate their right sides:

b²-x² = a²-(c-x)²
b²-x² = a²-(c²-2cx+x²)
b²-x² = a²-c²+2cx-x²
Add x² to both sides:
b² = a²-c²+2cx

From ߡADC, 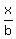 = cos(A) or x = b·cos(A)

Substituting that for x:

b² = a²-c²+2c·b·cos(A)

Isolate a² on the right side:

b² + c² - 2c·b·cos(A) = a²

That is equivalent to

a² = b²+c²-2·c·b·cos(A)

or since c·b = b·c,

a² = b²+c²-2·b·c·cos(A) 

-----------------------
The law of sines for this case

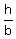 = sin(A) and  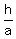= sin(B)

h = b·sin(A) and h =a·sin(B)

So  b·sin(A) = a·sin(B)

Divide both sides by sin(A)sin(B)

     = 

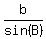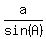That's not complete yet, for we haven't shown that those
equal to 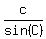 but it will be when we finish 
the next case. 

--------------------------------------------

a² = b²+c²-2·b·c·cos(A)  when ∠A is acute and ∠B is obtuse.



Extend AB and draw CD ⊥ AB.  Label CD h for the height of ߡABD.
Label the left part of c, AD as x and the right part of c DB as c-x.


 
ߡADC and ߡBDC are right triangles, so by the Pythagorean
theorem,

h² = b²-(c+x)² and also h² = a²-x²

Therefore equate their right sides:

b²-(c+x)² = a²-x²
b²-(c²+2cx+x²) = a²-x²
b²-c²-2cx-x² = a²-x²
Add x² to both sides:
b²-c²-2cx = a²

From ߡADC, 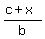 = cos(A)
           c+x = b·cos(A)
             x = b·cos(A)-c

Substituting in
b²-c²-2cx = a²

  b²-c²-2c(b·cos(A)-c) = a²
b²-c²-2·c·b·cos(A)+2c² = a²
    b²+c²-2·c·b·cos(A) = a²

That is equivalent to

a² = b²+c²-2·c·b·cos(A)

or since c·b = b·c,

a² = b²+c²-2·b·c·cos(A)
 
---------------------------
The law of sines for this case

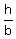 = sin(A) and  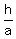= sin(∠CBD)

h = b·sin(A) and h =a·sin(∠CBD)

So  b·sin(A) = a·sin(∠CBD)

Divide both sides by sin(A)sin(∠CBD)

     = 

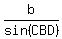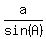Now we use the fact that the sine of an angle 
is equal to the sine of its supplement.  Therefore
if we erase the extended part we can label ∠CBD as ∠B.

     = 

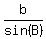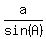The law of sines is now complete for the first case 
was for two angles being acute, and this case is for 
when one angle is obtuse.
Since the other two angles are necessarily acute, 
the first case takes care of them and we have the
complete law of sines:

 =  = 
  
------------------------------------

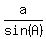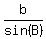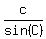To prove the law of cosines when A is an obtuse angle,
we have to accept the definition from xy-plane 
trigonometry that cos(180°-A) = -cos(A).

We'll just take the above triangle and swap angles 
A and B and sides a and b:




Extend BA and draw CD ⊥ BD.  Label CD h for the height of ߡABC.
Label the extended segment, AD, as x.


 
ߡADC and ߡBDC are right triangles, so by the Pythagorean
theorem,

h² = b²-x² and h² = a²-(c+x)²

Therefore equate their right sides:

b²-x² = a²-(c+x)²
b²-x² = a²-(c²+2cx+x²)
b²-x² = a²-c²-2cx-x²
Add x² to both sides:
   b² = a²-c²-2cx

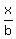From ߡADC,  = cos(CAD),
            x = b·cos(CAD)

and since ∠CAD and ∠BAC are supplementary,

cos(∠CAD) = -cos(∠BAC)
and
           x = -b·cos(∠BAC)

   b² = a²-c²-2cx

becomes:

   b² = a²-c²-2c[-b·cos(∠BAC)]

   b² = a²-c²+2c·b·cos(∠BAC)

Isolate a² on the right

   b²+c²-2c·b·cos(∠BAC) = a²

which is equivalent to
  
a² = b²+c²-2c·b·cos(∠BAC)

or since c·b = b·c,

a² = b²+c²-2·b·c·cos(∠BAC)

and if we erase the extended 
segment x, we can write ∠BAC as
∠A and have

a² = b²+c²-2·b·c·cos(A)

---------------------------
Edwin