Question 724170: The measure of an angle of a parallelogram is 18 degrees less than 5 times the measure of an adjacent angle. Explain how to find the measures of all the interior angles of the parallelogram.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! What you need to know is that the measures of adjacent interior angles of a parallelogram add up to  . (We can be fancy and say that adjacent interior angles of a parallelogram are supplementary). With that, you set up an equation. The rest is simple algebra. Once you find one angle, the measures of the adjacent ones can be calculated by subtracting the measure found from , and the fourth angle has the same measure as the first one.
 Angles 1 and 2 are adjacent interior angles of the blue parallelogram.
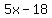Let's sat that angle 1 measures  degrees, and angle 2 measures "18 degrees less than 5 times the measure" of angle 1, so it measures  degrees.
Since angles 1 and 2 are supplementary,
 -->  -->  -->  -->  .
So angle 1 measures  ,
the adjacent angles measure 
WHY ADJACENT ANGLES ADD UP TO
In the drawing, angles 1 and 2 are adjacent interior angles of the blue parallelogram.
You might remember that when a line crosses two parallel line it forms eight angles, but among all those angles there will be at most two different measures, and measures that are not the same add up to .
In the drawing, the parallel horizontal lines and the slanted line that crosses them making the numbered angles, form a "family" of eight related angles. One half (four) of those angles are congruent to one another, and have the same certain measure, and the other group of four angles are also congruent to one another, and supplementary to the angles in the first group. So you have eight angles, but if you know the measure of one, you know the measure of all.
The pair of angles 2 and 3 are called vertical (to each other), and are known to be congruent (same measure). The same goes for angles 4 and 5.
The pair of angles 2 and 4 are called alternate interiors (to each other), and are also known to be congruent (same measure).
There are more names to describe the relation of one angle to another among those eight angles, but who needs to remember more names.
What matters is that angles 2, 3, 4, and 5 all have the same measure.
It is obvious that angles 4 and 5 are supplementary to angle 1.
Angle 2, having the same measure as 4 and 5, is also supplementary to angle 1.
|
|
|
