SOLUTION: What are the focus and directrix of the parabola with the equation y = 1/12x2? focus: (3, 0) ; directrix: y = –3 focus: (–3, 0) ; directrix: y = 3 focus: (0, 3) ; directrix:

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: What are the focus and directrix of the parabola with the equation y = 1/12x2? focus: (3, 0) ; directrix: y = –3 focus: (–3, 0) ; directrix: y = 3 focus: (0, 3) ; directrix:      Log On


   

Question 723666: What are the focus and directrix of the parabola with the equation y = 1/12x2?
focus: (3, 0) ; directrix: y = –3
focus: (–3, 0) ; directrix: y = 3
focus: (0, 3) ; directrix: y = –3
focus: (0, –3) ; directrix: y = 3
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
The standard equation for a parabola with its axis vertical is:
%28x+-h%29%5E2+=+4a%28y-k%29 ...(1)
The vertex is (h,+k).
The focus is (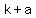h,+k+%2B+a).
The directrix is y+=+k+-a.
you have
y+=+%281%2F12%29x%5E2+...solve for x%5E2
y+%2F%281%2F12%29=+x%5E2+
12y+=+x%5E2 ....write it in form given above
12%28y-0%29+=+%28x-0%29%5E2+
as you can see
h=0
k=0
4a=12...=>...a=3
than,
the vertex is (h,+k)=(0,0)
the focus is (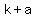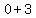h, k+%2B+a)= (0, 0+%2B+3)=(0,+3)
the directrix is y+=+k+-a...=>..y+=+0-3...=>..y+=-3
so, your answer is:
focus: (0,+3) ; directrix: y+=-3