Question 723103: Three numbers form an arithmetic sequence having a common difference of 4, if the first number is increased by 2, the second number increased by 3 and the third number by 5, the resulting numbers form a geometric sequence. Find the original numbers.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Let the number in arithmetic sequence with a common difference of 4 be
 ,  , and 
I assume that by "the first number" the problem means the smallest of them, which would be
If is increased by 2, we get
 .
If (the second number) is increased by 3 , we get
 .
If (the third number) is increased by 5, we get
Since the numbers  , , and 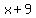 form a geometric sequence, the ratio of one number to the next is the same, meaning that
Equating the cross products (or, if you prefer, multiplying both sides of the equal sign times 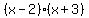 to eliminate denominators) we get
 -->  -->  -->  --> 
The original numbers are:
 and
|
|
|
