Question 722966: My daughter has a question on a chapter review that I cannot figure out. She is to factor and check 16x^2 + 81. If it were 16x^2-81, I could understand it as (4x+9)(4x-9) and that checks out, but I cannot seem to figure out the equation as it is written. Can you help me please?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!
If she has studied imaginary numbers she can factor it,
since i² = -1 and therefore
-i² = 1
16x² + 81 =
16x² + 81·1
Now substitute -i² for the 1
16x² + 81·(-i²)
16x² - 81i²
(4x - 9i)(4x + 9i)
However if she has not studied imaginary numbers, then she
should just write "prime".
Edwin
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! Using only real number, you cannot factor  ,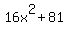
As you said
 can be factored, and when one or the other of those factors is zero (for x=9/4 or x=-9/4), their product is zero too, meaning  .
 or  can be factored too, and become zero when they have a zero factor.
If you could factor 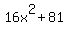using real numbers, you would be able to make it zero for some real value of x, and  would have a solution.
However, for real values of x,  and  cannot be zero.
Maybe your daughter is studying complex numbers, or maybe she is supposed to say it cannot be factored, or maybe there was a typo.
You can factor 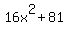using complex numbers, including the imaginary number  , whose square is 
|
|
|
