Question 722699: how to solve |log2(x÷6)|^(x^2-18x+56)>1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! There may be a shorter, more clever way to do this but here goes...
As you will soon see, we will be interested in when the exponent is positive and when it will be negative. (A zero exponent results in a 1 which is not greater than 1. So we factor it:

From this we can tell that...
If (x < 4 or x > 14), then 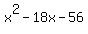 will be positive. will be positive.
and
if (x > 4 and x < 14), then 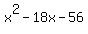 will be negative. will be negative.
(If you can't see this, then try some of these x's out.)
Now let's start the solution. We will break it down into cases that cover all possible values for the logarithm. (Note: To save space I am omitting the solution to some simple logarithmic inequalities from the main discussion of the solution. If you need to see these solutions, they are at the end.)- First of all, the argument of any log may not be zero or negative. In other words it must be positive. If x/6 > 0 then
x > 0 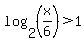 If this is true then any positive exponent will make the left side greater than 1. So we need to solve: If this is true then any positive exponent will make the left side greater than 1. So we need to solve:
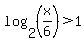 and exponent is positive. Or, using what we found earlier about the exponents: and exponent is positive. Or, using what we found earlier about the exponents:
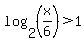 and (x < 4 or x > 14) and (x < 4 or x > 14)
Solving the log inequality we get:
x > 12 and (x < 4 or x > 14)
This resolves to just
x > 14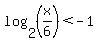 If this is true then the absolute value will be greater than 1. And again we will need a positive exponent. So: If this is true then the absolute value will be greater than 1. And again we will need a positive exponent. So:
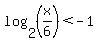 and (x < 4 or x > 14) and (x < 4 or x > 14)
x < 3 and (x < 4 or x > 14)
which resolves to:
x < 3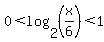 If this is true then the log (and its absolute value) is a positive, proper fraction. To make this greater than 1 we will need a negative exponent. So If this is true then the log (and its absolute value) is a positive, proper fraction. To make this greater than 1 we will need a negative exponent. So
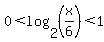 and (x > 4 and x < 14) and (x > 4 and x < 14)
Solving...
x > 6 and x < 12 and (x > 4 and x < 14)
which resolves to:
x > 6 and x < 12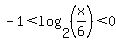 If this is true then the log is a negative proper fraction but its absolute value will be a positive, proper fraction. To make this greater than 1 we will again need a negative exponent. So If this is true then the log is a negative proper fraction but its absolute value will be a positive, proper fraction. To make this greater than 1 we will again need a negative exponent. So
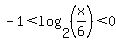 and (x > 4 and x < 14) and (x > 4 and x < 14)
Solving...
x > 3 and x < 6 and (x > 4 and x < 14)
which resolves to:
x > 4 and x < 6- The only possible values for the logarithm that we have not considered are 0, 1 and -1. If the log is equal to any of these numbers then the left side cannot possible be greater than zero because:
- If the log is zero, zero to any power cannot be greater than zero.
- If the log is 1 or -1, its absolute value will be a 1 and 1 to any power cannot be greater than one.
So we get no additional solutions with the log is 0, 1 or -1.
Putting this all together we get:
(0 < x < 3) [from cases 1 and 3]
or
(4 < x < 6) [from case 5]
or
(6 < x < 12) [from case 4]
or
(x > 14) [from case 2]
IOW: The solutions to the inequality are all positive numbers except 3, 4, 6, 12, 14, any number between 3 and 4 or any number between 12 and 14.
Solutions to the logarithmic inequalities:
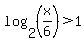
In exponential form:
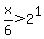
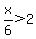
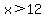
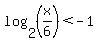
In exponential form:
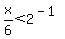


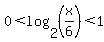
In exponential form:
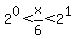

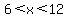
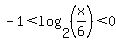
In exponential form:

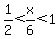
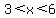
|
|
|