Question 722684: Maximum Profit: A chain store manager has been told by the main office that daily profit, P, is related to the number of clerks working that day, x, according to the function P = -25x^(2) + 300x. What number of clerks will maximize the profit, and what is the maximum possible profit?
1. Could you please explain and provide solutions to the above problem?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! daily profit, P, is related to the number of clerks working that day, x,
according to the function P = -25x^(2) + 300x.
What number of clerks will maximize the profit,
:
this is a quadratic equation with a neg coefficient of x^2,
so we know that the max is on the axis of symmetry
The formula for the axis of symmetry; x = -b/(2a), in this equation
a = -25, b = 300
so we have
x = 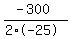
x = +6 clerks for max profit
:
"and what is the maximum possible profit?
Replace x with 6 in the original equation
p = -25(6^2) + 300(6)
p = -25(36) + 1800
p = -900 + 1800
p = $900 is the max profit
|
|
|