Question 720676: x^4-3x^3-x^2-27x-90=0 find the zeros
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
To find the zeros we need to factor the polynomial. The greatest common factor is 1 (which we rarely factor out). There are too many terms for factoring by patterns or for trinomial factoring. And there is an odd number of terms so factoring by grouping will be difficult, if not impossible. So we are left with factoring by trial and error of the possible rational roots.
The possible rational roots of a polynomial are all the ratios, positive and negative, that can be formed using a factor of the constant term on top and a factor of the leading coefficient on the bottom. The constant term (at the end) is 90. (Actually it's -90. But since we're going to include all positive and negative ratios, it doesn't make any difference if we use -90 or 90.) There are many factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 and 90. The leading coefficient (in front) is 1 (whose factors are 1's). This makes the list of possible rational roots:
+1/1, +2/1, +3/1, +5/1, +6/1, +9/1, +10/1, +15/1, +18/1, +30/1, +45/1 and +90/1
which simplify to:
+1, +2, +3, +5, +6, +9, +10, +15, +18, +30, +45 and +90
This is quite a long list. Finding one or more actual roots could take some time.
1 and -1 will always be possible rational roots and checking them can be done with mental math (since powers of 1 and -1 are fairly simple). Neither of these turn out to be roots. Checking the other possible rational roots is usually easiest by using synthetic division. (We use division because if r is a root then (x-r) is a factor. And if (x-r) is a factor then (x-r) will divide evenly into the polynomial.)
Trying 2:
2 | 1 -3 -1 -27 -90
--- 2 -2 -6 -66
-------------------------
1 -1 -3 -33 -156
The number in the lower right hand corner is the remainder. It is not zero so (x-2) is does not divide evenly, x-2 is not a factor and 2 is not a root.
Trying -2:
-2 | 1 -3 -1 -27 -90
---- -2 10 -18 90
-------------------------
1 -5 9 -45 0
The remainder is zero. So (x-(-2)) (or (x+2)) is a factor and -2 is a root. Not only that, but the rest of the bottom row tells us what the other factor is. The "1 -5 9 -45" translates into: 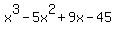 . So now our equation look like:
Now we see if 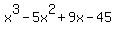will factor. We could continue to try possible rational roots (although the 90's are on longer possible). But 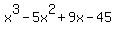has an even number of terms so factoring by grouping might work and, if it does, it will be probably be a lot easier than wading our way through the still long list of possible rational roots.
We have a second root/zero: 5 (from the (x-5) factor). The 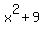 will not factor any further. But it is a quadratic so we can use the quadratic formula to find its zeros. I'll leave it up to you to work out the formula. But I can look at 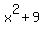and see that the zeros will be +3i.
So the four roots/zeros of are:
-2, 5, 3i and -3i
|
|
|
