SOLUTION: 6. A ball is thrown vertically upward with an initial velocity of 48 feet per second. The ball started from a height of 8 feet off the ground. a. At what time will the

The formula is

h(t) = h0 + v0t - 16t²

where 
h0 = starting height off the ground = 8 feet
v0 = the initial velocity (+ if up, - if down) = +48 ft/s
t = time in seconds
h(t) = the height when the time = t seconds.

So the equation becomes

h = h0 + v0t - 16t²
h = 8 + 48t - 16t²

Write in descending order

h(t) = -16t² + 48t + 8

This is the same as the equation of the parabola

f(x) = -16x² + 48x + 8

where f(x) represents the height h and x 
represents the time t

The parabola with equation 

f(x) = ax² + bx + c 
    
has vertex whose x-coordinate is 

where a = -16, b = 48, c = 8

So this parabola reaches its maximum height when

x =  =  =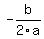 

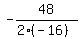And since x represents the time t, the ball will reach
its maximum height in  or 1.5 seconds.

That will be the height when when t = 1.5 seconds.

h(t) = -16t² + 48t + 8
h(1.5) = -16(1.5)² + 48(1.5) + 8
h(1.5) = 44 feet

h(t) = -16t² + 48t + 8
h(3) = -16(3)² + 48(3) + 8
h(1.5) = 8 feet high.  Notice that it will be back to the same 
height off the ground as the height it started at.

Here is the graph where x=t and y=h.  The green line
is the axis of symmetry and it is a vertical line going through
the vertex (1.5,44), so it's equation is x=1.5.



Edwin