Question 720143: please help me solve the following trigonometric equation using Pythagorean identity formula:
1-sin^2theta=0.5
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i will use the letter T to represent theta.
the pythagorean identify is sin^2(T) + cos^2(T) = 1
subtract sin^2(T) from both sides of this equation to get:
cos^2(T) = 1 - sin^2(T)
your equation is 1 - sin^2(T) = .5
since 1 - sin^2(T) is equivalent to cos^2(T), replace 1 - sin^2(T) with cos^2(T) and you get:
cos^2(T) = .5
take the square root of both sides of this equation to get:
cos(T) = +/- sqrt(.5)
cos(T) can be + sqrt(.5) or - sqrt(.5)
if + sqrt(.5), then T is equal to 45 degrees.
if - sqrt(.5), then T is equal to 135 degrees.
to find the angle whose cosine is equal to sqrt(.5), you use the cos^-1 function of your calculator.
the key to solving this, however, is to recognize that:
1 - sin^2(T)
is equivalent to cos^2(T) based on the pythagorean formula of:
sin^2(T) + cost^2(T) = 1.
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me solve the following trigonometric equation using Pythagorean identity formula:
1 - sin^2theta = 0.5
~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @Theo is incomplete, and therefore incorrect.
I came to provide a correct solution.
I will look for solutions in the interval [0°,360°), which represents the unit circle.
I will use the letter t to represent  .
The Pythagorean identify is sin^2(t) + cos^2(t) = 1.
You can write it in the form
cos^2(t) = 1 - sin^2(t).
You are given that 1 - sin^2(t) = 0.5.
Hence,
cos^2(t) = 0.5.
Take the square root of both sides of this equation to get:
cos(t) = +/- .
The Pythagorean identify is sin^2(t) + cos^2(t) = 1.
You can write it in the form
cos^2(t) = 1 - sin^2(t).
You are given that 1 - sin^2(t) = 0.5.
Hence,
cos^2(t) = 0.5.
Take the square root of both sides of this equation to get:
cos(t) = +/- 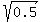 .
If cos(t) = + .
If cos(t) = + 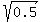 , then angle 't' is either 45° or -45°, which geometrically is the same as 315°.
If cos(t) = - , then angle 't' is either 45° or -45°, which geometrically is the same as 315°.
If cos(t) = - 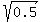 , then angle 't' is either 135° or 225°.
Thus, in the interval [0°,360°) the given equation , then angle 't' is either 135° or 225°.
Thus, in the interval [0°,360°) the given equation 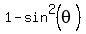 = 0.5 has 4 (four) solutions
that are 45°, 135°, 225° and 315°. = 0.5 has 4 (four) solutions
that are 45°, 135°, 225° and 315°.
Solved.
If a student losing the roots while solving such equation, as tutor @Theo did,
it is considered as a grave sin. The score is cut, and the student is sent for re-training.
And such teaching as presented in the post by @Theo is considered as unsatisfactory.
|
|
|